In my first 4 posts about Stata and Python, I confirmed you how one can arrange Stata to make use of Python, 3 ways to make use of Python in Stata, how one can set up Python packages, and how one can use Python packages. It is likely to be useful to learn these posts earlier than you proceed with this submit if you’re not acquainted with Python. Now, I’d prefer to shift our focus to some sensible makes use of of Python inside Stata. This submit will exhibit how one can use Stata to estimate marginal predictions from a logistic regression mannequin and use Python to create a three-dimensional floor plot of these predictions.
We can be utilizing the NumPy, pandas, and Matplotlib packages, so it’s best to test that they’re put in earlier than we start.
Predicted possibilities for continuous-by-continuous interactions
A number of years in the past, I wrote a Stata Information article titled Visualizing continuous-by-continuous interactions with margins and twoway contour. In that article, I match a logistic regression mannequin utilizing information from the Nationwide Well being and Vitamin Examination Survey (NHANES). The dependent variable, highbp, is an indicator for hypertension, and I included the primary results and interplay of the continual variables age and weight.
. webuse nhanes2, clear
. svy: logistic highbp c.age##c.weight
(working logistic on estimation pattern)
Survey: Logistic regression
Variety of strata = 31 Variety of obs = 10,351
Variety of PSUs = 62 Inhabitants dimension = 117,157,513
Design df = 31
F( 3, 29) = 418.97
Prob > F = 0.0000
--------------------------------------------------------------------------------
| Linearized
highbp | Odds Ratio Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
age | 1.100678 .0088786 11.89 0.000 1.082718 1.118935
weight | 1.07534 .0063892 12.23 0.000 1.062388 1.08845
|
c.age#c.weight | .9993975 .0001138 -5.29 0.000 .9991655 .9996296
|
_cons | .0002925 .0001194 -19.94 0.000 .0001273 .0006724
--------------------------------------------------------------------------------
Be aware: _cons estimates baseline odds.
The estimated odds ratio for the interplay of age and weight is 0.9994, and the p-value for the estimate is 0.000. Decoding this result’s difficult as a result of the percentages ratio is basically equal to the null worth of 1, however the p-value is basically zero. Is the interplay impact significant? It’s typically simpler to find out this by wanting on the predicted chance of the result at completely different ranges of the covariates quite than wanting solely at this odds ratio.
The code block beneath makes use of margins to estimate the anticipated chance of hypertension for all combos of age and weight for values of age starting from 20 to 80 years in increments of 5 and for values of weight starting from 40 to 180 kilograms in increments of 5. The choice saving(predictions, substitute) saves the predictions to a dataset named predictions.dta. I then use the dataset predictions, rename three variables within the dataset, and put it aside once more.
webuse nhanes2, clear
svy: logistic highbp age weight c.age#c.weight
quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
vce(unconditional) saving(predictions, substitute)
use predictions, clear
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
save predictions, substitute
In my earlier Stata Information article, I used graph twoway contour to create a contour plot of the anticipated possibilities of hypertension.
On this submit, I’m going to make use of Python to create a three-dimensional floor plot of the anticipated possibilities.
Utilizing pandas to learn the marginal predictions into Python
Python will need to have entry to the info saved in predictions.dta to create our three-dimensional floor plot. Let’s start by importing the pandas package deal into Python utilizing the alias pd. We are able to then use the read_stata() technique within the pandas package deal to learn predictions.dta right into a pandas information body named information.
. python:
-------------------------------------------- python (sort finish to exit) --------
>>> import pandas as pd
>>> information = pd.read_stata("predictions.dta")
>>> information
pr_highbp age weight
0 0.020091 20 40
1 0.027450 20 45
2 0.037401 20 50
3 0.050771 20 55
4 0.068580 20 60
.. ... ... ...
372 0.954326 80 160
373 0.958618 80 165
374 0.962523 80 170
375 0.966072 80 175
376 0.969296 80 180
[377 rows x 3 columns]
>>> finish
--------------------------------------------------------------------------------
We are able to then seek advice from a variable inside the information body by typing dataframe[‘varname‘]. For instance, we might seek advice from the variable age within the information body information by typing information[‘age’].
. python:
-------------------------------------------- python (sort finish to exit) --------
>>> import pandas as pd
>>> information = pd.read_stata("predictions.dta")
>>> information['age']
0 20
1 20
2 20
3 20
4 20
..
372 80
373 80
374 80
375 80
376 80
Title: age, Size: 377, dtype: int8
>>> finish
-------------------------------------------------------------------------------
We are able to seek advice from a number of variables inside an information body by typing dataframe[[‘varname1‘, ‘varname2‘]]. For instance, we might seek advice from the variables age and weight within the information body information by typing information[[‘age’, ‘weight’]].
. python:
-------------------------------------------- python (sort finish to exit) --------
>>> import pandas as pd
>>> information = pd.read_stata("predictions.dta")
>>> information[['age', 'weight']]
age weight
0 20 40
1 20 45
2 20 50
3 20 55
4 20 60
.. ... ...
372 80 160
373 80 165
374 80 170
375 80 175
376 80 180
[377 rows x 2 columns]
>>> finish
-------------------------------------------------------------------------------
Utilizing NumPy to create lists of numbers
We can even have to create lists of numbers to put ticks on the axes of our graph. Let’s import the NumPy package deal into Python utilizing the alias np. We are able to then use the arange() technique within the NumPy package deal to create lists. The instance beneath creates a listing of numbers named mylist starting at 20 and ending at 90 in increments of 10.
. python: -------------------------------------------- python (sort finish to exit) -------- >>> import numpy as np >>> mylist = np.arange(20,90, step=10) >>> mylist array([20, 30, 40, 50, 60, 70, 80]) >>> finish -------------------------------------------------------------------------------
It’s possible you’ll be shocked that the ensuing checklist doesn’t embody the quantity 90. This isn’t a bug or a mistake. It’s a characteristic of the arange() technique in NumPy. You may sort np.arange(20,100, step=10) if you happen to want to embody 90 in your checklist.
Utilizing Matplotlib to create three-dimensional floor plots
Now, we’re able to create our plot. Let’s start by importing the NumPy, pandas, and Matplotlib packages into Python.
python:
import numpy as np
import pandas as pd
import matplotlib
finish
Let’s additionally import the pyplot module from the Matplotlib package deal utilizing the alias plt. The brand new line is proven in crimson to make it simpler to determine.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
finish
I’ve added the assertion matplotlib.use(‘TkAgg’) to the code block beneath. I would like this assertion in order that Matplotlib will run accurately utilizing Python in my Home windows 10 atmosphere. Matplotlib makes use of completely different rendering engines for various functions and for various platforms. It’s possible you’ll want to make use of a special rendering engine in your computing atmosphere, and you’ll study extra within the Stata FAQ titled “How do I exploit Matplotlib with Stata?“.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
finish
Subsequent, we are able to use the read_stata() technique within the pandas package deal to learn predictions.dta right into a pandas information body named information.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
finish
Then, we are able to use the axes() technique within the pyplot module to outline a three-dimensional set of axes named ax.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
finish
Subsequent, we are able to use the plot_trisurf() technique within the pyplot module to render our three-dimensional floor plot.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
ax.plot_trisurf(information['age'], information['weight'], information['pr_highbp'])
finish
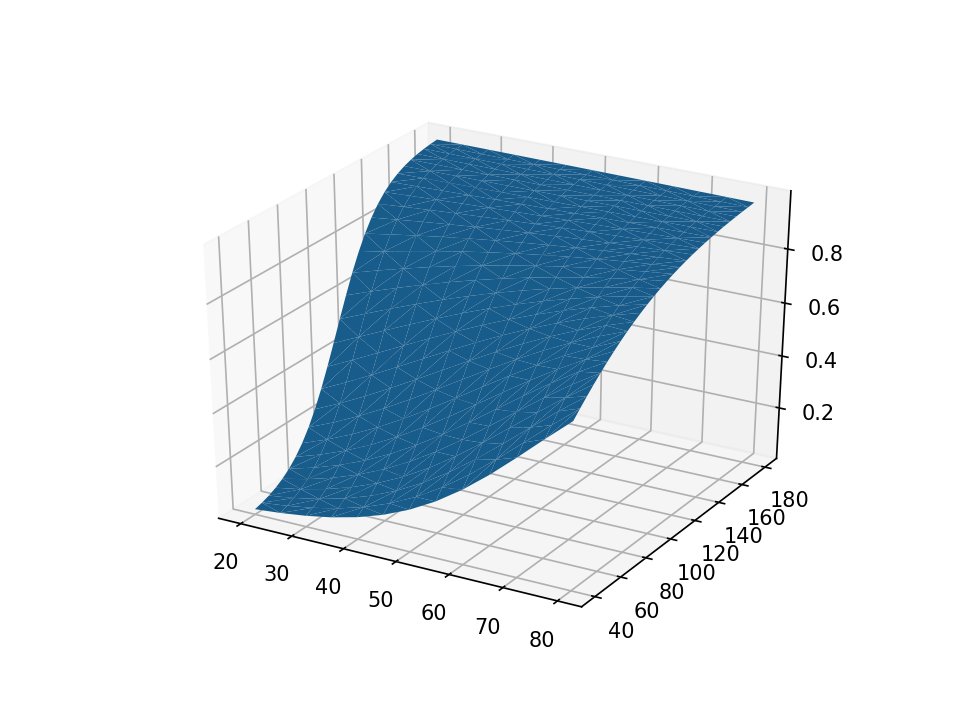
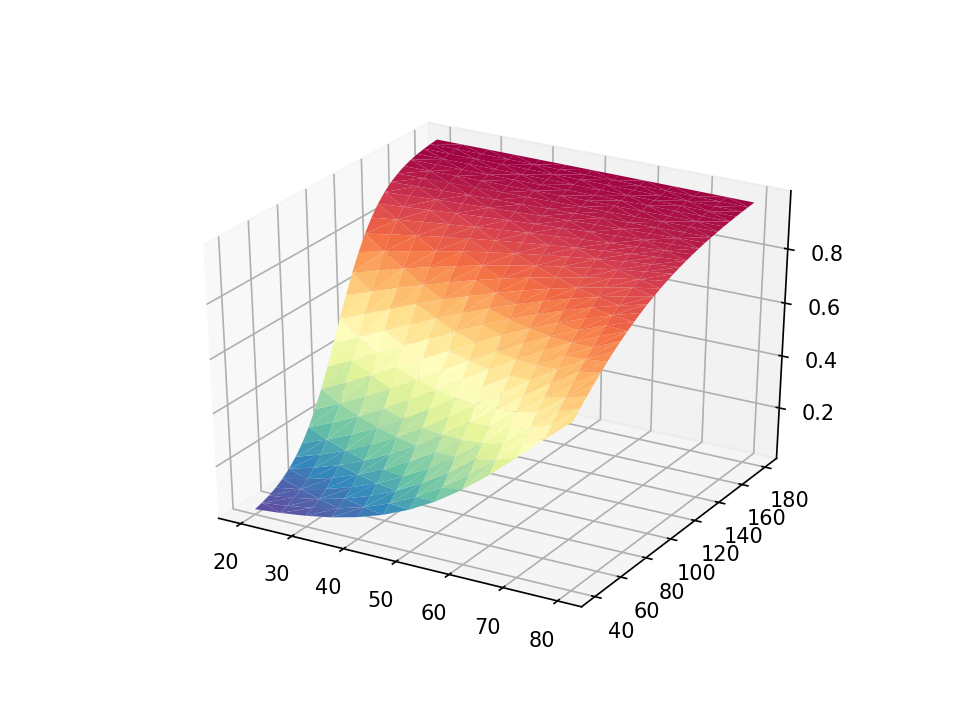
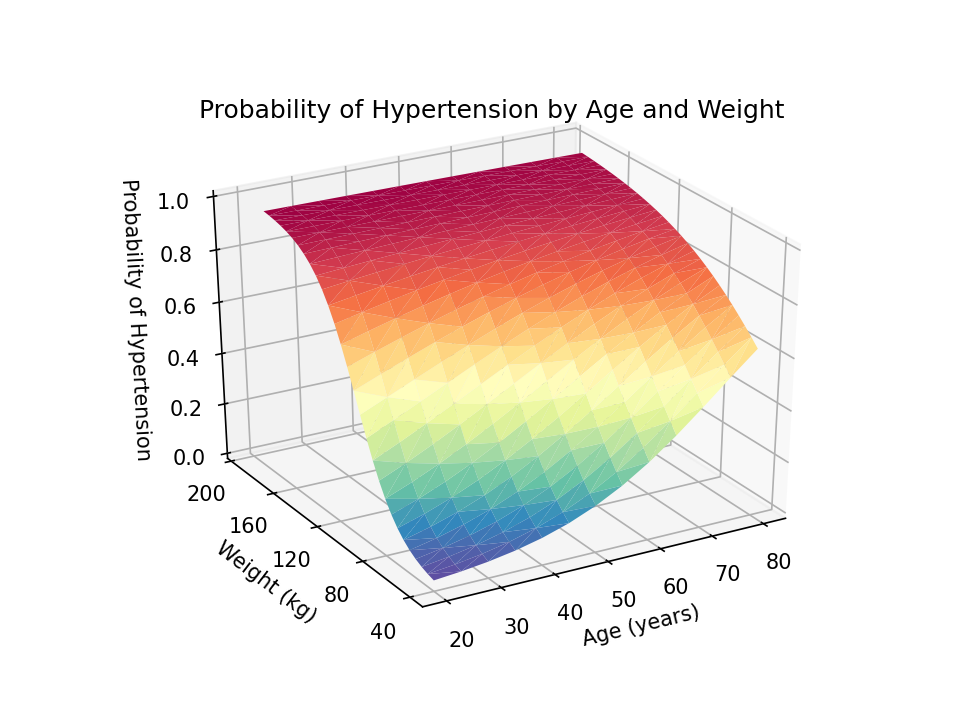
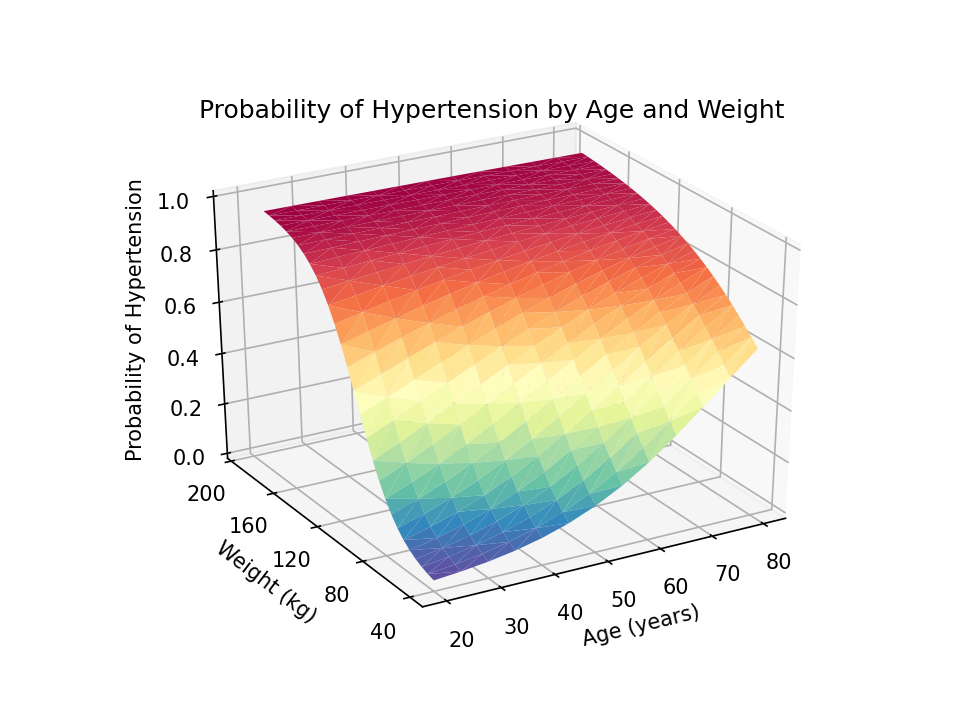
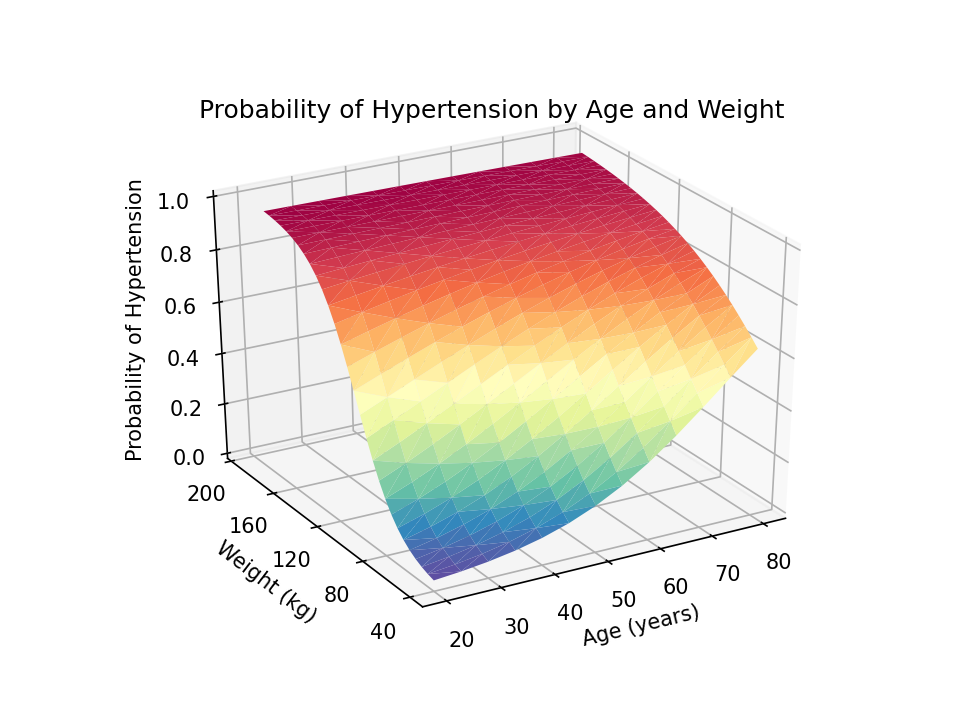
The floor plot is rendered with strong blue by default. Let’s use the cmap=plt.cm.Spectral_r choice so as to add shade shading to our plot. The colour scheme Spectral_r shows decrease possibilities of hypertension with blue and better possibilities with crimson.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
ax.plot_trisurf(information['age'], information['weight'], information['pr_highbp'],
cmap=plt.cm.Spectral_r)
finish
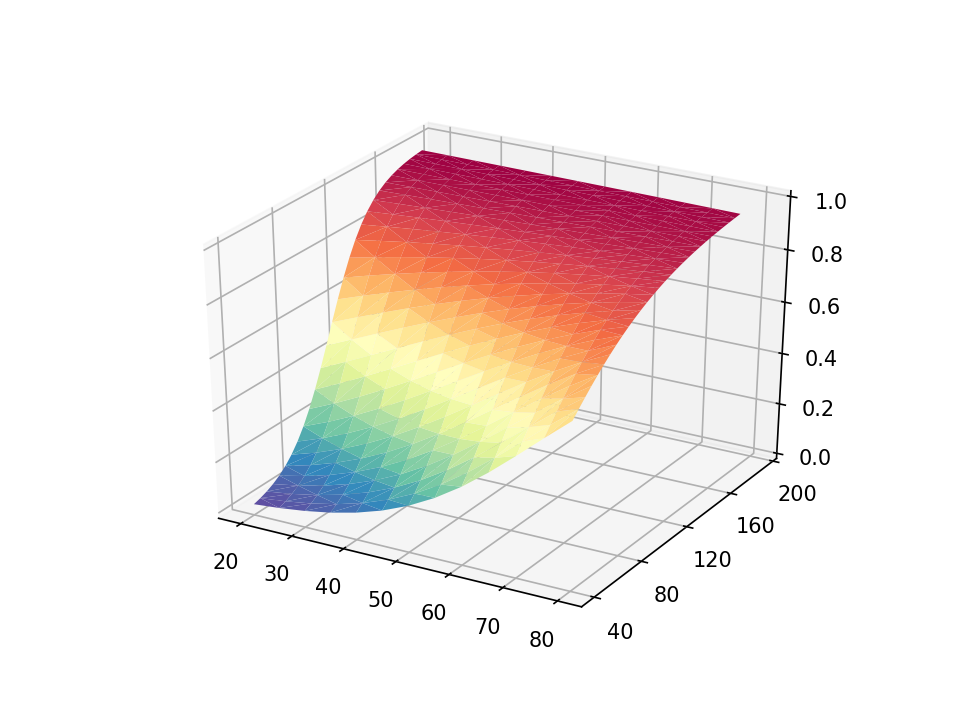
The default axis ticks look affordable, however we might want to customise them. The y axis seems to be considerably cluttered, and we are able to modify the increment between ticks with the set_yticks() technique within the axes module. The arange() technique within the NumPy module defines a listing of numbers from 40 to 200 in steps of 40. We are able to use comparable statements so as to add customized tick marks to the x and z axes.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
ax.plot_trisurf(information['age'], information['weight'], information['pr_highbp'],
cmap=plt.cm.Spectral_r)
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
finish
Subsequent, we are able to add a title to our graph with the set_title() technique within the axes module. And we are able to add labels to the x, y, and z axes with the set_xlabel(), set_ylabel(), and set_zlabel() strategies, respectively.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_title("Chance of Hypertension by Age and Weight")
ax.set_xlabel("Age (years)")
ax.set_ylabel("Weight (kg)")
ax.set_zlabel("Chance of Hypertension")
finish
You may alter the view angle utilizing the view_init() technique. The elev choice adjusts the elevation, and the azim choice adjusts the azimuth. Each are laid out in levels.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_title("Chance of Hypertension by Age and Weight")
ax.set_xlabel("Age (years)")
ax.set_ylabel("Weight (kg)")
ax.set_zlabel("Chance of Hypertension")
ax.view_init(elev=30, azim=240)
finish
I would favor to learn the z-axis title from backside to high quite than high to backside. I can change this utilizing a mix of the set_rotate_label(False) technique and the rotation=90 choice within the set_xlabel() technique.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_title("Chance of Hypertension by Age and Weight")
ax.set_xlabel("Age (years)")
ax.set_ylabel("Weight (kg)")
ax.zaxis.set_rotate_label(False)
ax.set_zlabel("Chance of Hypertension", rotation=90)
ax.view_init(elev=30, azim=240)
finish
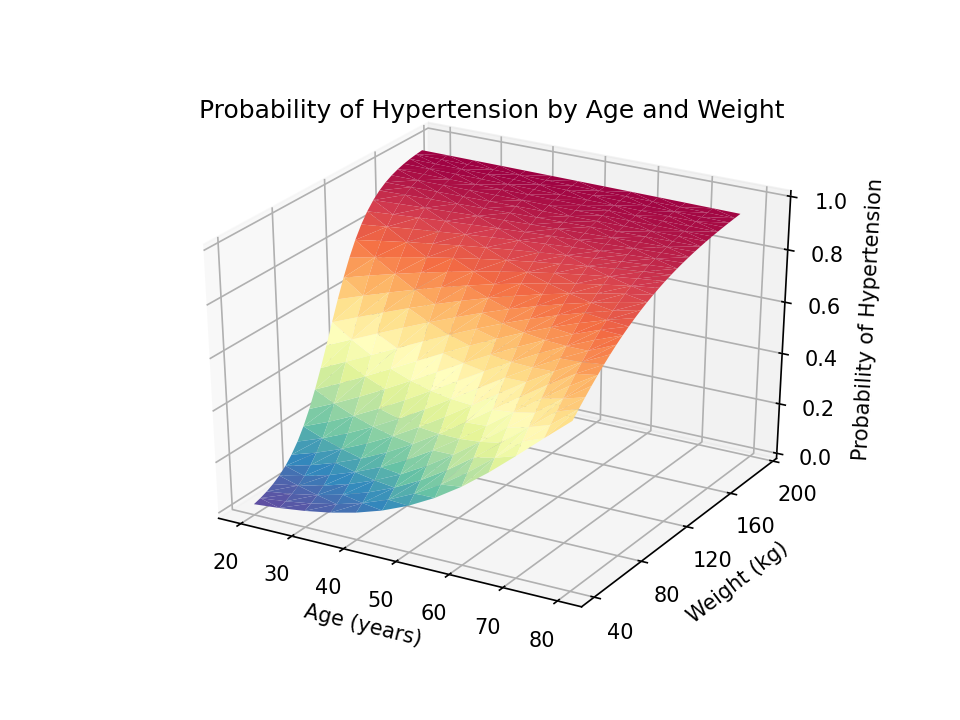
Lastly, we are able to use the savefig() technique to save lots of our graph as a transportable community graphics (.png) file with 1200 dots-per-inch decision.
python:
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
information = pd.read_stata("predictions.dta")
ax = plt.axes(projection='3d')
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_title("Chance of Hypertension by Age and Weight")
ax.set_xlabel("Age (years)")
ax.set_ylabel("Weight (kg)")
ax.zaxis.set_rotate_label(False)
ax.set_zlabel("Chance of Hypertension", rotation=90)
ax.view_init(elev=30, azim=240)
plt.savefig("Margins3d.png", dpi=1200)
finish
Conclusion
The ensuing three-dimensional floor plot exhibits the anticipated chance of hypertension for values of age and weight. The possibilities are indicated by the peak of the floor on the z axis and by the colour of the floor. Blue signifies decrease possibilities of hypertension, and crimson signifies increased possibilities of hypertension. This is usually a helpful technique to interpret the interplay of two steady covariates in a regression mannequin.
I’ve collected the Stata instructions and Python code block right into a single do-file beneath. And I’ve included feedback to remind you of the aim of every assortment of instructions and statements. Be aware that Stata feedback start with “//”, and Python feedback start with “#”.
instance.do
// Match the mannequin and estimate the marginal predicted possibilities with Stata
webuse nhanes2, clear
logistic highbp c.age##c.weight
quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
saving(predictions, substitute)
use predictions, clear
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
save predictions, substitute
// Create the three-dimensional floor plot with Python
python:
# Import the mandatory Python packages
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TkAgg')
# Learn (import) the Stata dataset “predictions.dta”
# right into a pandas information body named “information”
information = pd.read_stata(“predictions.dta”)
# Outline a 3-D graph named “ax”
ax = plt.axes(projection=’3d’)
# Render the graph
ax.plot_trisurf(information[‘age’], information[‘weight’], information[‘pr_highbp’],
cmap=plt.cm.Spectral_r)
# Specify the axis ticks
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
# Specify the title and axis titles
ax.set_title(“Chance of Hypertension by Age and Weight”)
ax.set_xlabel(“Age (years)”)
ax.set_ylabel(“Weight (kg)”)
ax.zaxis.set_rotate_label(False)
ax.set_zlabel(“Chance of Hypertension”, rotation=90)
# Specify the view angle of the graph
ax.view_init(elev=30, azim=240)
# Save the graph
plt.savefig("Margins3d.png", dpi=1200)
finish