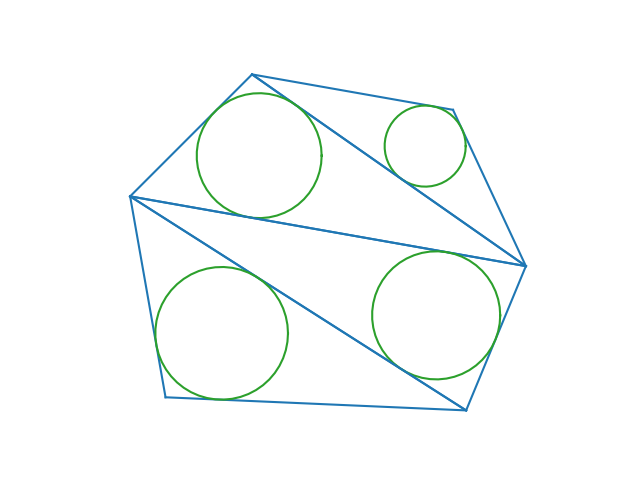
Right here’s an fascinating theorem that results in some aesthetically pleasing photographs. It’s often known as the Japanese cyclic polygon theorem.
For all triangulations of a cyclic polygon, the sum of inradii of the triangles is fixed. Conversely, if the sum of inradii is unbiased of the triangulation, then the polygon is cyclic.
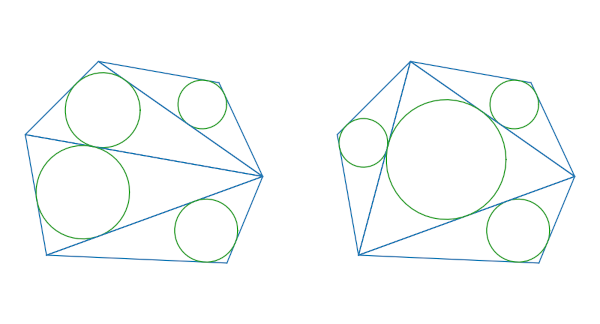
The picture above exhibits two triangulations of an irregular hexagon. By the top of the put up we’ll see the code that created these photographs, and we’ll see another triangulations. And we’ll see that the sum of the radii of the circles is similar in every picture.
Glossary
In case any of the phrases within the theorem above are unfamiliar, right here’s a fast glossary.
A triangulation of a polygon is a option to divide the polygon into triangles, with the restriction that the triangle vertices come from the polygon vertices.
A polygon is cyclic if there exists a circle that passes by means of all of its vertices. By the way, if a polygon has n + 2 sides, the variety of doable triangulations is the nth Catalan quantity. Extra on that right here.
The inradius of a triangle is the radius of the biggest circle that matches contained in the triangle. Extra on internal and outer radii right here.
Equations for inradius and incenter
We’d wish to illustrate the theory by drawing some photographs and by including up the inradii. This implies we want to have the ability to discover the inradius and the incenter.
The inradius of a triangle equals its space divided by its semiperimeter. The realm we are able to discover utilizing Heron’s formulation. The semiperimeter is half the perimeter.
The incenter is the weighted sum of the vertices, weighted by the lengths of the other sides, and normalized. If the vertices are A, B, and C, then the incenter is
the place A is the vertex reverse facet a, B is the vertex reverse facet b, and C is the vertex reverse facet c.
Python code
The next Python code will draw a triangle with its incircle. Calling this perform for every triangle within the triangulation will create the illustrations we’re after.
from numpy import *
import matplotlib.pyplot as plt
def draw_triangle_with_incircle(A, B, C):
a = linalg.norm(B - C)
b = linalg.norm(A - C)
c = linalg.norm(A - B)
s = (a + b + c)/2
r = sqrt(s*(s-a)*(s-b)*(s-c))/s
middle = (a*A + b*B + c*C)/(a + b + c)
plt.plot([A[0], B[0]], [A[1], B[1]], colour="C0")
plt.plot([B[0], C[0]], [B[1], C[1]], colour="C0")
plt.plot([A[0], C[0]], [A[1], C[1]], colour="C0")
t = linspace(0, 2*pi)
plt.plot(cos(t) + middle[0], sin(t) + middle[1], colour="C2")
return r
Subsequent, we choose six factors not fairly evenly spaced round a circle.
angle = [0, 50, 110, 160, 220, 315] # levels p = [array([cos(deg2rad(angle[i])), sin(deg2rad(angle[i]))]) for i in vary(6)]
Now we draw three completely different triangulations of the hexagon outlined by the factors above. We additionally print the sum of the inradii to confirm that every sum is similar.
def draw_polygon(triangles):
rsum = 0
for t in triangles:
rsum += draw_triangle_with_incircle(p[t[0]], p[t[1]], p[t[2]])
print(rsum)
plt.axis("off")
plt.gca().set_aspect("equal")
plt.present()
draw_polygon([[0,1,2], [0,2,3], [0,3,4], [0,4,5]])
draw_polygon([[0,1,2], [2,3,4], [4,5,0], [0,2,4]])
draw_polygon([[0,1,2], [0,2,3], [0,3,5], [3,4,5]])
This produces the 2 photographs on the prime of the put up the one beneath. All of the inradii sum are 1.1441361217691244 with somewhat variation within the final decimal place.