I talked with two editors this week and it received me considering of one thing simple that might be performed that doesn’t appear terribly controversial. So what I’m going to do on this put up is lay that out, with some fairly footage, and a few math to make a degree. That is associated to a put up I wrote a pair weeks in the past. Solely this time I’m going to say that if Claude Code helps economists full their manuscripts quicker, then it’s borderline not possible that we don’t see swells in increased charges of submissions at journals and subsequently extra refereeing per particular person.
Thanks once more for supporting the substack and the podcast! It’s a number of enjoyable speaking about causal inference and AI, notably Claude Code. For those who aren’t a paying subscriber, take into account turning into one so you’ll be able to learn an ungodly variety of outdated posts about difference-in-differences, causal inference and AI, together with my Claude Code collection, all of which is behind the paywall! All new Claude Code posts are free, however go behind the paywall after 4 days, so proceed stopping by for the free content material too!
Claude Code and Bathtubs
Derek Neal and Armin Rick wrote a paper about prisons. The US incarceration fee rose from about 160 per 100,000 within the early Seventies to over 500 per 100,000 by 2008. The jail inhabitants tripled. Individuals handled this as a sociological puzzle. It glided by phrases like mass incarceration, the brand new Jim Crow, and has been thought of a uniquely American pathology. And there are deep financial and sociological tales to inform. However Neal and Rick’s paper accommodates additionally a quite simple arithmetic perception which is that the extending sentences should trigger the inventory of prisoners to develop even if you happen to by no means enhance the arrest fee or the conviction fee. In different phrases, longer sentences are sufficient to explode the nation’s incarceration fee.
Consider the jail system as a tub. Water flows in by the tap and exits by the drain. The tap, the stream in, are admissions, which is a perform of crime, arrests, convictions and sentences upon conviction. Water flows out by the drain which is jail releases and that features folks ending their sentences in addition to early launch by parole. The water stage within the tub is the jail inhabitants and in equilibrium, given mounted jail capability, when admissions and releases have been equal, the jail inhabitants didn’t change past some manageable fluctuations right here and there.
So, what if you happen to have been to extend the speed of water getting into the bath, maybe by widening the tap. In our state of affairs that might imply arresting extra folks however holding conviction charges mounted. You then’d have extra convictions, extra stream. However one other method you might do it’s with harder sentencing, that means enhance the conviction fee for a similar group of arrestees. And but nonetheless yet another mechanism is maintain arrest charges the identical and conviction charges the identical, however prolong the sentence for just about each crime by a number of years.
Neal and Rick suggest that the final mechanism — longer sentences — was liable for the jail inhabitants per capita to rise by as a lot because it did in American historical past and in such a brief time frame. And because it was exactly longer sentences, it almost mechanically pressured the discharge fee to get tousled in such a method that at a given time frame, there must be extra prisoners within the prisons. You can not enhance the stream in by longer sentences and launch them on the similar fee per interval since you might be modifying the discharge fee per interval by extending the sentence size.
And in order such, the stock-flow id they suggest during which the inventory tomorrow equals the inventory at present plus the influx minus the outflow states that this specific opening up the nozzle ended up each widening the stream in and saved the again finish flat, inflicting the inventory to rise, and that as a result of this was an id, it couldn’t be in any other case.
I wrote my 2007 dissertation on the financial results of mass incarceration on Black households and Black marriage markets, so the precise phenomena itself was not new to me once I learn Neal and Rick. What was new for me was this express break down of shares and flows, and the mathematical necessity of rising jail populations through one specific stream channel (longer sentences). For some purpose, all the mechanisms — increased arrest charges, increased conviction charges, longer sentences — have been in my thoughts roughly equivalent. And to a level they for certain are, little question. All of them widen the stream in, however in precept you might concurrently enhance arrest charges and enhance parole charges and even cut back sentences and subsequently the rise in admissions and departures may cancel out and thus maintain mounted the jail inhabitants. However the truth that longer sentences tied up the backend stream out has been one thing I’ve considered lots for a decade since I learn the paper.
And now I’m fascinated about this stock-flow id as a result of I believe tutorial journals are about to study the identical lesson whether or not Claude Code causes the market to have AI totally automated papers like what the Social Catalyst Lab is illustrating in Zurich, or if it merely makes economists extra productive such that they every end their papers quicker. Both of those triggers elevated flows, and since we have now a hard and fast variety of referees which can’t be expanded by AI, AI should enhance the variety of manuscripts per referee and manuscripts per journal. Which may threaten the system fully.
As I mentioned, that is associated to an earlier put up I wrote. Two weeks in the past I laid out what occurs when AI collapses the price of producing a submission-quality manuscript. Submissions multiply. Publication slots don’t. Acceptance charges crash. It’s a prisoner’s dilemma — individually rational to scale quantity, collectively harmful. You possibly can learn the complete argument in Submit 27.
However whereas this put up is said, it’s nonetheless considerably totally different. Submit 27 was the financial story about ceteris paribus technological shocks to provide curves resulting from marginal value of manufacturing plummeting to zero, unchanging demand curves, and equilibrium. Pretty simple story you’ll be able to plot out in a couple of strikes utilizing solely generic data of provide and demand.
However now I wish to discuss on this put up is in regards to the plumbing. Particularly the stock-flow id. And I’m doing this as a result of I don’t assume you’ll be able to argue with an id because it’s not a mannequin, not a theorem, and never a conjecture. It’s accounting and should maintain subsequently because of this.
And but the put up is definitely nonetheless totally different as a result of in contrast to put up 27, this one is normative, not merely constructive. It’s prescriptive, not merely descriptive. It accommodates as economists say “coverage suggestions” round normative objectives that I believe might be the objectives that unite all economists, even ones who oppose AI for analysis. And it’s written for editor-in-chiefs, co-editors, affiliate editors and editorial boards to ponder. I wished to only put it on the market as I believed it is perhaps helpful to assist launch conversations internally at journals amidst themselves.
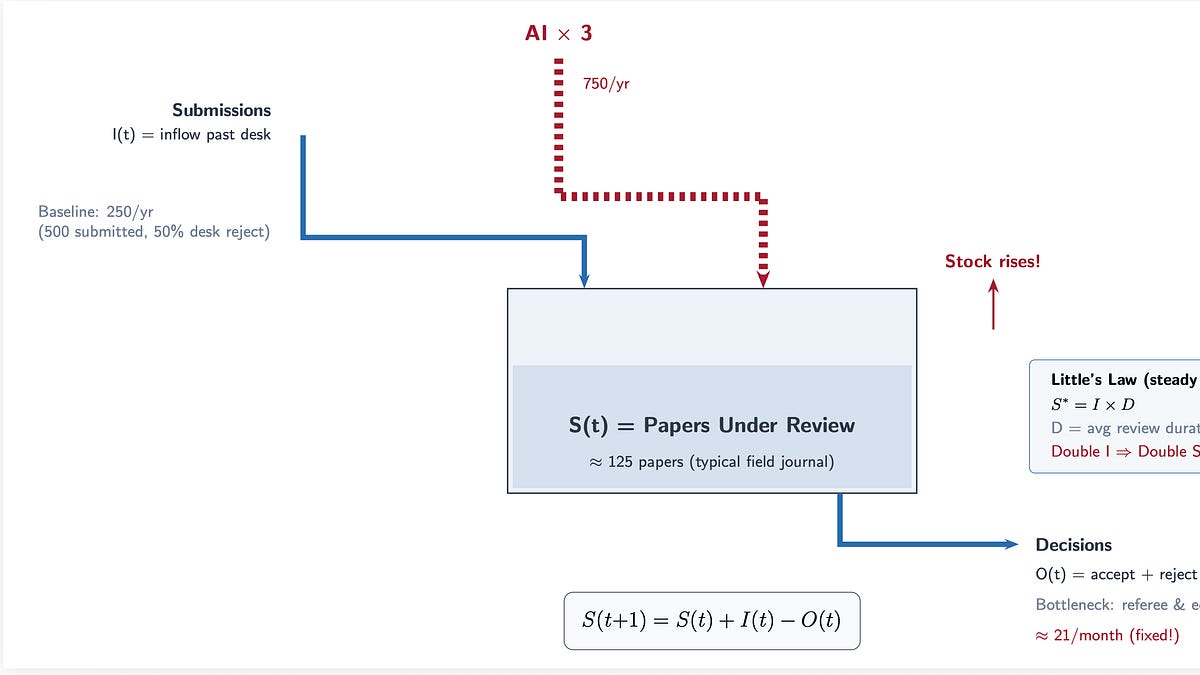
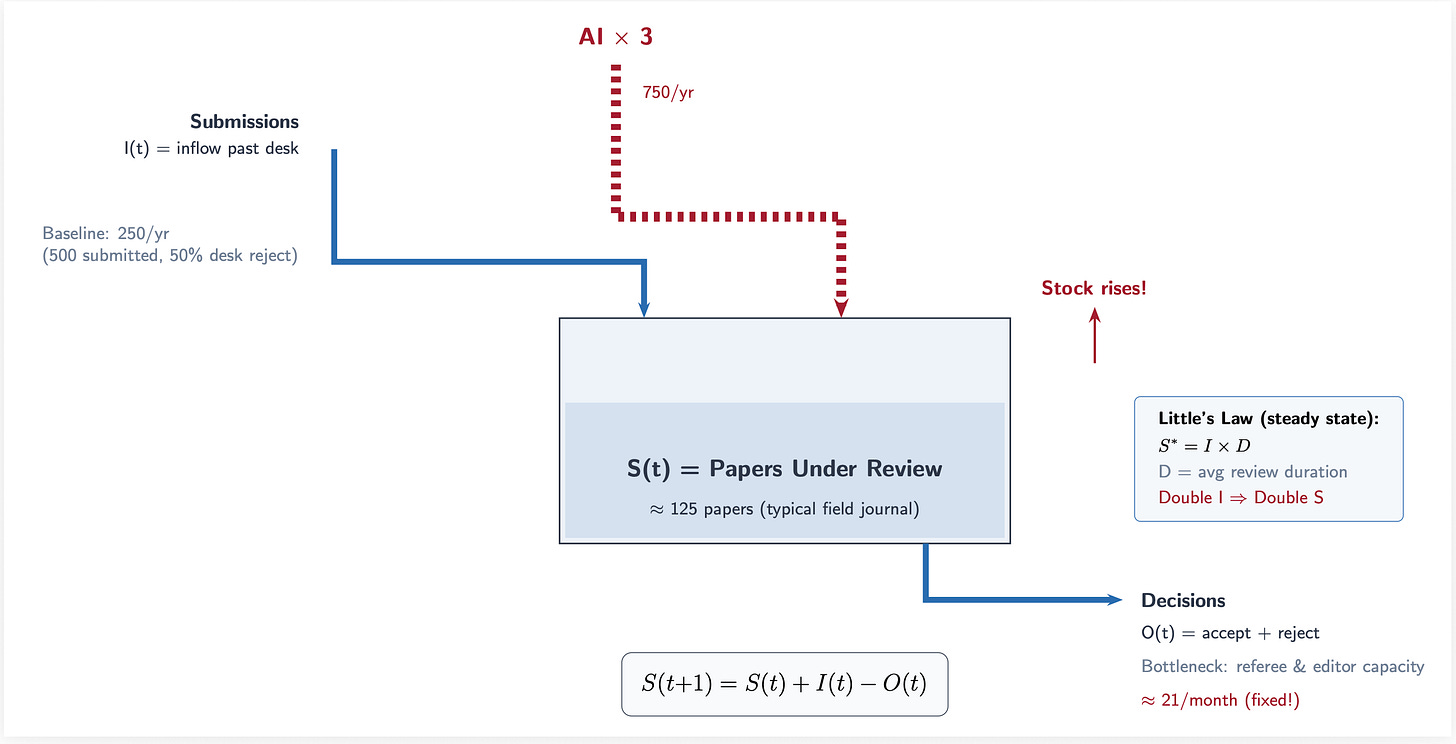
First, let me write down the stock-flow id from Neal and Rick and get that out of the way in which. It’s a dynamic id the place t is at present.
(S(t+1) = S(t) + I(t) – O(t))
S is the inventory of papers at present beneath evaluation at a journal. I is the influx that are new submissions that to the desk. O is the outflow which on this case are editorial choices on the desk, referee choices, settle for, reject, or R&R. The inventory tomorrow, S+1, equals the inventory at present, t, plus what got here in, I, minus what went out, O.
In regular state, influx equals outflow and thus the inventory settles at S* = I instances D, the place D is the typical time a paper spends within the evaluation course of. That’s “Little’s Legislation” which is identical equation that governs hospital beds, freeway site visitors, and jail populations. In different phrases, it’s Little’s Legislation utilized to scientific manuscripts.
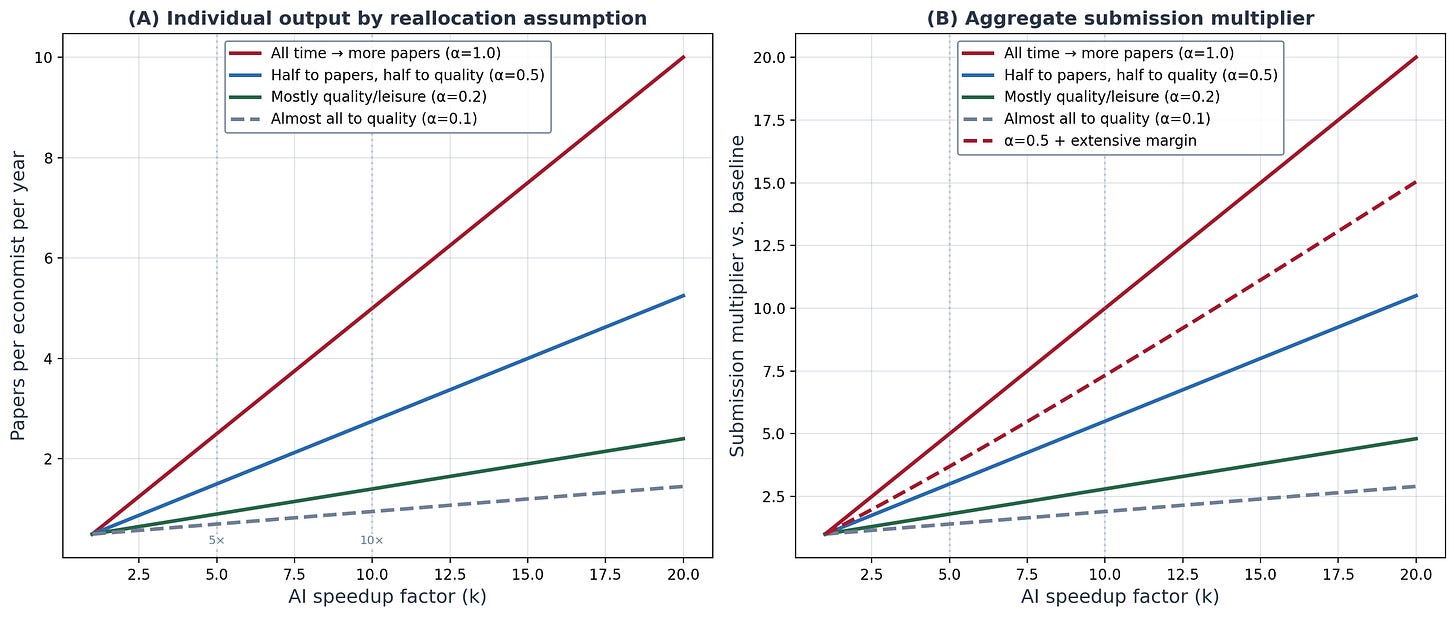
And herein lies the issue, if you wish to name it a real downside: AI will increase I. It does this by elevated labor productiveness. Economists, on this instance, end papers quicker, inflicting them to put in writing extra papers, inflicting them to submit extra papers at every time interval.
However D is bottlenecked by referees. There are solely so many of those people and so they take a number of weeks to a number of months to judge a paper except AI accelerates that course of too. And subsequently O is bottlenecked by editors who’re additionally people who can solely course of so many selections per week. So if I doubles and O stays flat, the inventory should develop. This leads to queuing. Wait instances to listen to again prolong and/or acceptance charges fall. Editors are taxed through elevated dealing with of submissions on a weekly foundation, and so submissions per editor rises, and in the event that they desk reject on the similar fee, submissions per referee does as properly. The denominator, in different phrases, stays mounted and fairly frankly can’t go up with out extra PhDs being introduced into economics, which editors and referees don’t management, however relatively is managed by state budgets, college allocation of funds to economics departments, extra college strains, and subsequently a development within the pool of school to edit journals and referee them as properly. However the former requires extra editors, which is a journal determination, and it finally doesn’t matter anyway as since every particular person is now submitting — not publishing, thoughts you, however submitting — at a better fee, even the expansions nonetheless should carry in additional papers per capita. The one factor you are able to do if I rises and also you need the inventory the identical is desk reject at a better fee, however even then that won’t change the inventory of submissions to the desk. Even if you happen to reject extra regularly on the desk, it gained’t matter with respect to the inventory of these manuscripts on the desk. Editors should be dealing with extra manuscripts per capita if I rises. The one method you might enhance submissions however keep the identical variety of manuscripts on the desk is that if there was some intermediate step between when an writer submits their manuscript however one thing intervenes earlier than it hits the desk — which makes completely no sense on this context, and subsequently AI should mechanically put extra papers into the mailbox of editors.
So, as I mentioned, this isn’t a mannequin in any respect. It’s an id, it’s going to maintain. The query is subsequently what’s going to the editors do on this state of affairs as a result of in the event that they do nothing in any respect, it’s going to merely cross alongside extra work to referees, who’re mounted, and it’s unclear if you’ll have the identical stage of compliance since you actually have heterogenous compliance now as it’s. The identical ones submitting at a better fee, experiencing increased productiveness, will nonetheless need to discover a approach to deal with the elevated influx to them managing extra papers per time interval irrespective of the way you slice it.
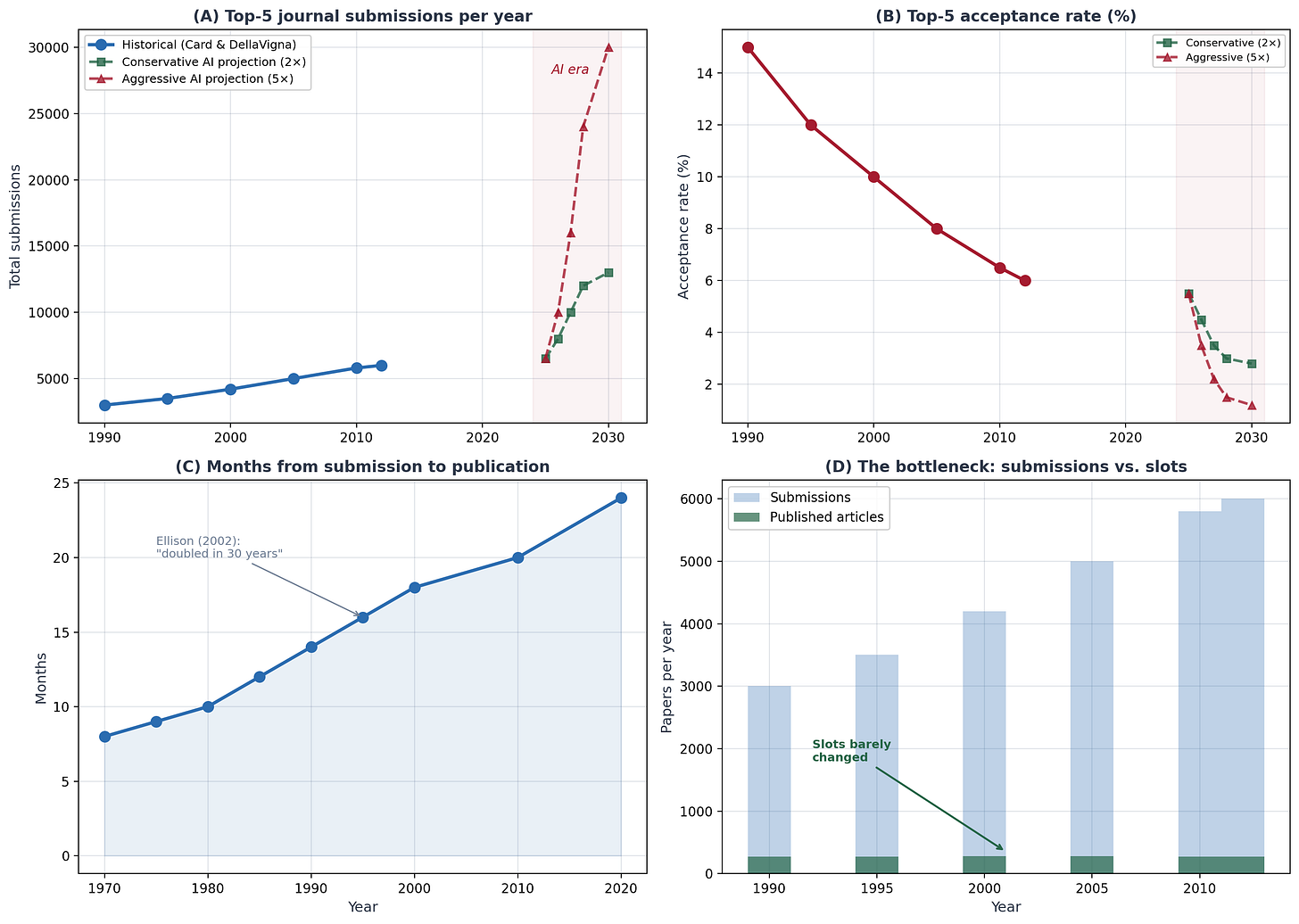
Card and DellaVigna documented this in 2013. Submissions to the top-5 journals almost doubled between 1990 and 2012 from about 3,000 to six,000 per yr. Over the identical interval, the variety of articles these journals truly printed fell from round 400 to 300. This led to acceptance charges collapsing from 15% to six%.
Time from submission to publication doubled too. Ellison measured this in a 2002 JPE, and it’s solely gotten worse since as a result of papers at the moment are thrice longer than they have been within the Seventies.
So right here’s the half that issues for the AI argument. Conley and Onder within the JEL discovered that 90% of economics PhDs by no means publish even half a paper in high journals. You could have Pareto legal guidelines governing the distribution of publication with the highest 1% of publishing economists produce round 13% of all quality-adjusted analysis. The highest 20% produce 80% which is the traditional ratio for the so-called Pareto precept.
Let’s take a look at a few of these numbers rearranged. Whole submissions have been rising from 1990 to 2010 (panel A) and beneath AI labor productiveness, if predictions are even moderately correct, might result in 2 to 5x that fee which is proven within the shaded pink area. Be aware that that is solely for the top-5s, whereas my earlier put up had been about all the journals. Acceptances charges on the high 5 (panel B) has been falling already, and subsequently that slope falls much more with AI beneath both conservative of aggressive eventualities. The rise in months from submission to publication continues rising (panel C) and subsequently the bottleneck happens with none change (panel D).
That is all pushed by elevated inflows, I. And within the stock-flow id and Little’s Legislation, it cascades by the system. Elevated strain at each stage. And since we have been already in a reasonably sturdy and difficult equilibrium as it’s due partly to our bigger papers, longer time to writing them, and problem cracking high journals, solely worsens the bottleneck.
Which implies that AI doesn’t create an issue, however relatively worsens an already current downside. And if labor productiveness is even modest, the bottleneck can actually break by elevated refusals by referees which causes much more issues. All of that is coming from manufacturing whereas maintaining analysis the identical. This has nothing but to do with publication.
The one lever editors can pull shortly is desk rejection. Ship extra papers again with out evaluation. Right here’s the arithmetic.
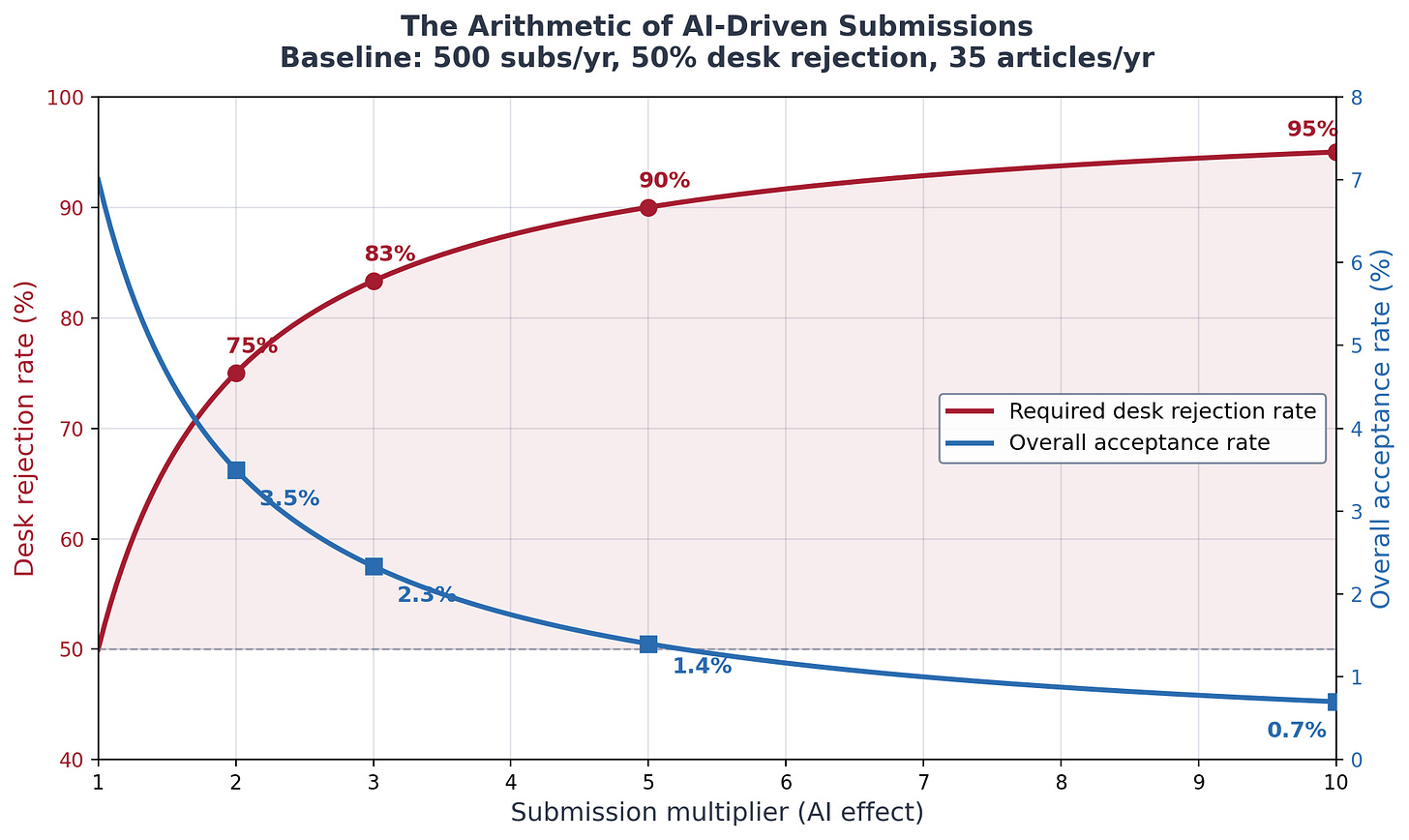
To maintain the evaluation queue secure when submissions multiply by some issue okay, it is advisable enhance desk rejection sufficient to carry the stream into evaluation fixed. The components is straightforward: the brand new desk rejection fee equals one minus the amount one minus the outdated fee divided by okay.
From what I can collect based mostly on the time I’ve to put in writing this and the sources I’ve at my disposal, I’m going to only assume that the standard subject journal (e.g., Journal of Labor Economics) at present desk-rejects about half its submissions. Any quantity will work, however I’ll use that as my instance for now. So assuming that that’s roughly true, then right here’s what occurs subsequent.
To maintain the inventory fixed on referees, at 2x submissions, desk rejection has to rise from 50% to 75%. At 3x, from 50% to 83%. At 5x, from 50% to 90%. At 10x, to 95%.
Thus a subject journal at present getting about 10 submissions per week who with AI see submission develop three-fold now see 30 per week. The editor would wish to desk-reject, subsequently, round 5 out of each six papers which suggests they’re triaging six papers per workday simply on the desk stage, earlier than any precise studying occurs.
As I mentioned within the earlier put up, although, this isn’t simple. The heuristics editors have traditionally use to make such fast choices are being weakened by AI, too. Why? As a result of the submissions are higher. Discipline journals typically publish papers with publicly out there knowledge, and as they’re additionally causal in nature, following methodological formulation resulting from repeated refinement over time, there’s an abundance of them within the coaching knowledge, and AI know present to put in writing them properly.
Some high subject journals (I gained’t title names) are as excessive as 90% difference-in-differences papers alone over the past decade. Diff-in-diff particularly follows a daily rhythm utilizing regularly geographic stage variation in insurance policies, typically publicly out there knowledge, introduced occasion research, and with these sturdy diff-in-diff estimators having tens of hundreds of citations, are methodologically superior too. And as these are current, and given economists put up working papers religiously, these two are within the coaching knowledge.
Which implies AI has roughly plotted the rhetoric of causal inference right down to the letter. And thus the heuristics of desk rejecting these kinds of papers is gone. Editors don’t simply take a look at papers which might be carried out poorly and rejected in a second. They don’t seem to be methodologically “non credible” papers and rejecting shortly. They’re increased high quality papers throughout the board, making it a lot more durable to desk reject.
Thus the quality-quantity composition on the desk has shifted immensely, and the noise to sign ratio collapsed. The AI-assisted papers will now be more durable to desk-reject. It’s not, in different phrases, merely that there are extra of them — it’s that there are extra and higher on a per submission foundation. They’ll be higher written, higher formatted, with clear code and virtually actually longer with extra appendices because of the capability to carry out each single robustness examine conceivable.
And so the sign that used to assist editors triage shortly equivalent to sloppy writing, lacking tables, manifestly apparent reasoning errors will disappear. Each paper will look competent on the floor, and the lengthy left tail of high quality will disappear. It’s going to not appear like the traditional distribution because the chance mass beneath the density will simply be this massively thick left tail at minimal, and because the desk reject determination is off the left tail, it is not going to be simply discernible what to reject in any respect as a result of, mockingly, these are higher manuscripts! Editors could be rejecting higher manuscripts! Which defeats the whole function of the journal’s existence within the first place. It is extremely onerous to justify a purpose of rejecting extra of higher scientific manuscripts when the purpose of science is to publish extra of these, not fewer.
Which implies that the editor must learn extra fastidiously to differentiate those with real contributions from those which might be simply well-polished nothing. However since AI almost certainly is particularly augmenting the production-side of employees with much less talent, there’s truly no purpose to reject extra of them. If something, they’ll need cross alongside extra of them as a result of beneath counterfactual with out AI that’s what they’d be doing after they would have seen this manuscript!
You see how all this logic is simply canceling out the outflow and thus the stock-flow id is forcing the inventory to rise? Forcing the manuscripts to rise into account? Forcing the manuscripts per referee to rise? And thus straining the bottleneck, probably to extinction?
Most of my earlier evaluation targeted on the intensive margin — current researchers producing extra papers. A productive economist going from two manuscripts a yr to 6. However I believe the intensive margin could also be larger, and it’s the half that actually scares me.
Keep in mind Conley and Onder’s numbers. 90% of PhDs barely publish. There’s a large inhabitants of individuals with graduate coaching, knowledge entry, analysis questions, and institutional affiliations who at present produce roughly zero papers per yr. Not as a result of they lack concepts. As a result of the execution value was prohibitive. They educate 4 programs a semester. They don’t have RA budgets. They haven’t touched Stata since their dissertation. The mounted value of organising a analysis mission — studying the newest estimator, cleansing the info, debugging the code, producing the tables — was just too excessive relative to the time they’d out there.
AI eliminates that mounted value. Adjuncts at instructing schools. Coverage researchers at assume tanks. Authorities economists at federal businesses. Grad college students who beforehand wanted two years of coursework earlier than they may produce something. Researchers in growing nations with out institutional assist.
This isn’t speculative. A 2025 evaluation in Science discovered that 36% of manuscripts submitted within the first half of 2024 already contained AI-generated textual content. Solely 9% disclosed it. Additionally see this one.
Researchers utilizing generative AI are publishing extra papers is my level.
The intensive margin so to talk was already activating even earlier than Claude Code, and it’s clearly Claude Code that’s the most productiveness enhancing technological shock as in contrast to conventional LLMs like ChatGPT, AI Brokers don’t simply discuss — they primarily do issues. And it’s the “doing of issues” that’s the actual transformation of employee’s manufacturing features resulting from lowered time use with concurrently higher coding practices, fewer errors, higher reasoning, and higher writing, all of which results in much less time per manuscript.
If even a fraction of the 80% of economists who at present produce virtually nothing begin submitting one paper a yr, the mixture impact dwarfs something the intensive margin can do, however virtually actually the intensive margin will expertise its personal change in productiveness. However simply take into consideration that Pareto precept for a minute — 80% of all PhD economists is a large amount of economists. Which is whether or not are actually easy eventualities the place this stacks up and quick — particularly in gentle of fixing labor markets normally.
Simply to call two, we have now federal cuts to overhead resulting in smaller college budgets resulting in fewer strains. And we have now start cohorts getting smaller every year after the Nice Recession inflicting universities to get a double whammy by decreasing enrollment cohorts, and thus decreasing tuition income too. Thus on the intensive margin, given the desirability of school jobs, virtually actually a race ensues amongst youthful cohorts, resulting in much more pressure on referees who’re older.
The Enrollment Cliff and the Lacking Infants: Who Wasn’t Born?
Right now’s put up is paywalled courtesy of coin flips. It’s a bit totally different than. regular, nevertheless it’s one thing I’ve been fascinated about relating to declining fertility and better training. Get pleasure from! And take into account turning into a paying subscriber!Scott’s Mixtape Substack is a reader-supported publication. To obtain new posts and assist my work, take into account turning into a free or paid subscriber.
So, with that out of the way in which, right here’s the place I wish to spend the remainder of this put up. As a result of I believe the prognosis from earlier plus the stock-flow id above is basically proper, I believe it’s now important to throw out concepts, if solely to present concepts to editor-in-chiefs, co-editors, affiliate editors and editorial boards. Even when these concepts are rejected, they hopefully will be subjects for consideration, and by me posting them, perhaps defuse among the awkwardness that individuals might really feel about even bringing it up. So I’m glad to throw out some concepts.
What ought to editors truly do?
And I’ve 4 proposals, ranked by how shortly they might be applied.
Earlier than any prescription, editors must have a dialog that they could not have been planning to have and should even haven’t wished to have. What’s the journal’s goal perform? What’s peer evaluation truly for? Why ought to this journal exist? What’s the value to society if it doesn’t exist. Such conversations are sometimes grouped beneath a enterprise faculty phrase referred to as “the worth proposition” and it refers to articulating clearly the financial worth of the services or products itself. And so the journal should try this, and encourage its employees (and doubtless its constituents, which is the whole occupation, however let’s simply concentrate on employees because the transaction prices are decrease to do it there, plus they’re those managing the influx and incurring the useful resource prices from peer evaluation).
It’s vital to have this dialog first, and be clear in regards to the determined upon goal perform, as a result of all coverage suggestions stream from it, and there are not less than two totally different solutions to it, and they’re utterly unique of the opposite.
The primary reply is AI prohibition. It goes one thing like this.
AI-generated analysis is basically unethical. It violates one thing about what scholarship means, even when the violation is difficult to articulate exactly. It needs to be banned. It’s based mostly on stolen work.
You will see quite a lot of moral and philosophically rooted claims across the AI prohibition viewpoint. It’s possible you’ll even discover the seemingly deserted “labor principle of worth” buried inside it since LLMs have been educated on economists’ and programmers’ personal time intensive prior work, and thus typically triggers claims that LLMs commit fixed piracy.
Beneath the AI prohibition goal, the best coverage is detection: construct instruments to establish AI-written manuscripts and reject them. And many economists really feel this fashion. I’m informed the social media platform, Bluesky, consists of a excessive proportion of economists who really feel strongly this fashion, and little question they’re a passionate and articulate group of economists which might be however the tip of the iceberg.
I wish to say one thing that I believe issues: these economists should be inspired to talk up, and their place should be genuinely revered. Possibly that goes with out saying, however many issues that go with out saying benefit saying it to ascertain the norm anyway. I don’t imply feigning respect too. I don’t imply “being well mannered”. I imply respect, which is lively listening, understanding, being affected person, not interrupting, and interacting critically with every particular person even and particularly when one strongly disagrees with what’s being mentioned. Economists as lots are clever folks pushed by a need to do proper by their science, and in the event that they consider AI in analysis is flawed, that perception deserves an actual listening to.
The second reply is to acknowledge, although, that the aim of peer evaluation, and subsequently the justification for each journal’s existence, is decidedly not to assist anybody preserve their job. The aim of peer evaluation is not to assist economists get tenure. It’s not to assist them enhance their incomes and wealth, get prizes, improve their status. It’s not to assist them in a quest to place extra strains on their vita.
We didn’t collectively invent peer evaluation, and science itself, as a way to construct a journal system as a way to make use of employees. In actual fact, using employees and satisfying their interior needs is irrelevant.
Peer evaluation was not invented as some Keynesian experiment like constructing bridges to nowhere.
The total function of peer evaluation and journals is to propel science ahead by innovation, correct info, and higher theories about the true world. And in economists’ personal fashions like Paul Romer’s endogenous development principle, the current Nobel work on inventive destruction, the huge literature on the Industrial Revolution and what ended millennia of stagnation, it’s a fixed theme that concepts and science are what produced falling mortality, rising wealth, and broadly shared enhancements in high quality of life. The so-called hockey stick of human progress is a current phenomenon, overlaying perhaps 0.01% of our species’ timeline. It seems pushed by science, literacy, numeracy, and public coverage choices that harness all three. Acemoglu and Johnson’s Energy and Progress makes this case at e-book size.
These two goal features produce utterly totally different insurance policies. If the purpose is to dam AI, you spend money on detection. If the purpose is to extend scientific innovation, and subsequently to play our half within the mission that bent the curve of human welfare, then you definitely spend money on analysis infrastructure that may deal with extra science, quicker, no matter the way it was produced.
I’ll state my place plainly. I consider the second needs to be our purpose. I don’t assume the purpose is to establish AI-generated manuscripts. I believe the purpose is to extend the speed of scientific innovation by cautious analysis and propagation by coverage and training. And the three proposals that comply with are grounded in that goal perform.
If LLMs induced the flood, undertake LLMs to assist type it. That is the quickest lever and the best one to implement.
Utilizing an LLM screening layer earlier than human evaluation may examine whether or not the tables match the textual content will instantly flag issues. It may confirm that code runs and reproduces the acknowledged outcomes. It may flag statistical crimson flags equivalent to miscalculated p-values, robustness checks that seem complete however check nothing significant, incorrectly calculated normal errors, identification methods that don’t truly establish something. It may even be educated on the editor’s tastes.
LLM screening doesn’t change human judgment. Fairly, LLLM screening provides the editor a triage “pre-desk report” to allow them to spend 5 minutes as an alternative of thirty on fast desk-reject determination. At 30 submissions per week, that’s the distinction between a manageable workload and drowning.
One can simply debate this coverage, however I might simply level out that the stock-flow id is an accounting id. One thing should be performed if we’re to take care of our analysis methods. So preserve that in thoughts.
The irony is that the software inflicting the issue can also be the very best software for managing it. If an Claude Code can write a paper, then it will possibly completely additionally critically learn one and it will possibly learn thirty within the time it takes an editor to learn one. So the query is whether or not editors are prepared to make use of it, and my guess is that those who undertake early will survive this transition, and I believe survival is a minimal prerequisite for peer evaluation to persist. Those who insist on studying each submission themselves will possible burn out and if it’s a journal coverage, then alternative might be tough, and you almost certainly invite unfavourable choice on the high and all through the editorial pool.
That is the highest-value, lowest-cost intervention, and I believe it issues much more than LLM screening. We needs to be requiring each writer to submit their code at submission, and to put up their mission on publicly out there repos too. We’re a long time into a serious empirical disaster round credibility, and the explanations to not require this at all times contain researchers wanting monopoly rights over their concepts. Which is ok, however as soon as the paper is prepared for submission, as a way to salvage the system, we want the code in order that we will confirm its accuracy even earlier than we ship it out.
And Claude Code can audit code extraordinarily properly, when one is expert sufficient to know learn how to do it, with out even the info.
So if each submission should embrace a working code repository that reproduces all outcomes from uncooked knowledge, a number of issues occur concurrently. First, it raises the price of submitting half-baked, faux papers that haven’t been verified by the human authors forward of time. A code repo that really runs requires actual knowledge and actual computation, not simply well-formatted LaTeX. Requiring this is able to enhance the standard of science, velocity it up, and because it makes use of LLMs for checking high quality first, it’s going to help referees by signaling that main issues have already been checked. The referee Bayesian updates upon receiving her task realizing that it has already gone by a code audit, and thus the cognitive load of fascinated about that exact type of hallucination is not less than vanishingly small. And if the referee can actually see the code, they’ll additionally examine for fundamental syntax errors themselves.
Some journals already require knowledge and code deposits for accepted papers. The AER has performed this for years. Journals will completely preserve falling swimsuit if they aren’t already. So this requirement additionally accelerates the whole publication course of by getting authors into the behavior of producing replicable code, and given the marginal value of replication has additionally dropped to zero, it helps authors take critically that they too are in all probability going to be targets by swarms of individuals trying to take down a manuscript.
My proposal is to not require replication. Fairly it’s to require it replicable supply code at submission, versus simply acceptance. Transfer the replication bundle requirement from the top of the pipeline to the start and also you in all probability mechanically tackle among the abuses of AI which is papers which have zero human contact and thus zero human verification anyplace.
The objection I anticipate is that this creates an additional burden on authors. However if you happen to wrote the paper with Claude Code, the code repository already exists. And if you happen to haven’t, then you’ll do it anyway. Higher get it out of the way in which. The marginal value of packaging it’s small to roughly zero, notably if you happen to use Claude Code that will help you. The one folks for whom that is genuinely expensive are those who don’t have working code, and people are precisely the submissions you wish to display out.
Present submission charges vary from zero to $800 like some finance journals. Most subject journals cost $100 to $300 relying on one’s membership to the neighborhood affiliation the journal is related to. These numbers are negligible.
And but they’re now too low.
A journal receiving 500 submissions per yr at $150 every collects $150 every collects $75,000 which is barely sufficient to pay a part-time editorial assistant. At $500 per submission, that′s $250,000 which is sufficient to fund one or two further affiliate editors. At 3x quantity, the income triples even with out elevating costs. With each quantity will increase and modestly increased charges, journals may construct the editorial capability they want.
Charges are a Pigouvian tax on the externality every submission creates as a result of each paper has an actual useful resource value in a system with peer evaluation. That useful resource value is referee time. Referee time has a possibility value, which is foregone scientific innovation. Thus to ship a manuscript prices society not simply the editor’s but additionally three to 5 referees’ their time, and the writer doesn’t pay these prices — notably if they’re performing automation.
However I wish to be trustworthy in regards to the distributional considerations. A blanket enhance to $500 falls hardest on junior college with out grants, researchers at instructing establishments, students in lower-income nations. Any charge enhance possible wants value discrimination equivalent to pupil charges, LMIC waivers, reductions for lively referees. ReStud already does a few of this, with lowered charges for early-career researchers. Though this can be a double-edged sword given it’s extremely possible that youthful cohorts can have much less antipathy to utilizing AI for his or her work, and thus might generate extra of it (notably given analysis discovering AI having giant beneficial properties to the least skilled employees), value discrimination can nonetheless assist the journals resolve how they wish to go about this or if the uniform pricing mannequin is greatest for them.
And even at 500, the anticipated worth calculation nonetheless works. A single high−subject publication is value a tenure case, a 500, a $20,000 increase, a presently discounted lifetime of elevated wealth. 5 hundred {dollars} is noise towards that payoff. So charges alone gained’t clear up this. However charges plus code repos plus LLM screening collectively create a friction gradient that’s proportional to paper high quality and forces authors to wager on their greatest papers and never merely play a lottery and throw as many strains into the ocean as they’ll. Dangerous papers get caught by the code examine. Marginal papers get caught by the LLM display. Solely papers that cross a MB-MC check will find yourself imposing useful resource prices on a human editor’s time, and those who do attain it, might be producing extra income which editors can use to make future adjustment planning.
Joshua Gans wrote a considerate response to Submit 27, and I wish to have interaction with it actually. His argument, roughly: the equilibrium will regulate. Increased charges, new journals, new norms, higher AI that improves high quality not simply amount. The market will type it out.
I agree with on all three. In the long term, the occupation will adapt. New establishments will emerge. AI will get higher at each producing and evaluating analysis. However in fact, in the long term, we’re additionally all useless.
It’s the transition dynamics which might be the issue. Neal and Rick’s jail analogy once more is useful. The US jail system did finally adapt . It did so by constructing extra prisons which value upwards of $80 billion a yr. The human value throughout the adjustment was staggering and doubtless not notably thought out given the jail growth chosen on some teams greater than others creating their very own loops from labor market scarring and recidivism. The truth that a system reaches a brand new equilibrium doesn’t imply the transition was painless nor that the brand new equilibrium is the very best one. It additionally doesn’t suggest that the invisible hand operates absent human intervention — the invisible hand occurs through human intervention, relatively.
My private opinion is that editors don’t have the luxurious of ready for the long-run equilibrium. They’ve been getting extra and longer submissions for a very long time, and it’s onerous to concurrently maintain the place that Claude Code will increase economists’ productiveness and in some way not enhance output. And if it will increase output, it’s not possible beneath this stock-flow id for it to not enhance manuscripts per editor and manuscripts per referees.
So to me, the query isn’t whether or not the market will type it out finally. It’s what you do proper now, this spring, this summer time, 2026, when the queue is already rising as a part of longer traits, the instruments persevering with to enhance, economists realizing en masse and shortly simply how radically transformative AI brokers will be, and the clocks ticking.
As I mentioned in put up 27, for many of the historical past of educational economics, the binding constraint on science was manufacturing. It was onerous to do analysis. It took time, and it notably took economists a very long time for regardless of the purpose. That is evidenced by our low annual manufacturing in comparison with psychology or medication. Our papers are longer, we usually don’t unfold the contribution out over a number of papers however relatively stick them into one paper, requiring fully totally different types of rhetoric and construction and techniques to cope with contradictions.
It’s onerous to scrub knowledge, notably giant surveys and administrative knowledge. Each of those can take an incredible period of time and for very totally different causes. The econometrics is continually evolving and researchers are anticipated to make use of them. And it’s onerous for everybody to put in writing clearly, and subsequently altogether it’s onerous to provide the completed product that constitutes a journal submission. The complete institutional equipment like PhD applications, analysis assistants, seminar tradition, the gradual tempo of publishing, was designed across the assumption that producing good work was costly.
And now, on daily basis, that assumption is being relaxed. Manufacturing is getting low-cost. That’s an empirically verifiable reality.
The binding constraint is shifting to analysis, which is to say it’s shifting from manufacturing to determining which analysis is sweet, which paper is modern.
And that’s a basically totally different downside requiring shifts in institutional designs. The editorial system was designed for a world the place manufacturing was costly and analysis was the bottleneck solely on the very high. Now, within the new world, manufacturing is reasonable and analysis is comparatively dearer. Wherever outflows are fixed, there’s now a bottleneck — not simply on the AER, however on the JHR, at JOLE, at Financial Inquiry, at each journal within the lengthy tail.
The query isn’t whether or not we should always count on AI for use in analysis. That ship sailed. To say in any other case is to dwell in denial. The query is whether or not we design establishments that may deal with what AI produces or whether or not we let the queue develop till the system breaks beneath its personal weight.
I don’t assume editors have a lot time to resolve. So I submit this put up to editors for his or her consideration, and anybody else .