(newcommand{mub}{{boldsymbol{mu}}}
newcommand{eb}{{boldsymbol{e}}}
newcommand{betab}{boldsymbol{beta}})Figuring out the stationarity of a time collection is a key step earlier than embarking on any evaluation. The statistical properties of most estimators in time collection depend on the info being (weakly) stationary. Loosely talking, a weakly stationary course of is characterised by a time-invariant imply, variance, and autocovariance.
In most noticed collection, nonetheless, the presence of a pattern part ends in the collection being nonstationary. Moreover, the pattern may be both deterministic or stochastic, relying on which acceptable transformations have to be utilized to acquire a stationary collection. For instance, a stochastic pattern, or generally generally known as a unit root, is eradicated by differencing the collection. Nonetheless, differencing a collection that in truth accommodates a deterministic pattern ends in a unit root within the moving-average course of. Equally, subtracting a deterministic pattern from a collection that in truth accommodates a stochastic pattern doesn’t render a stationary collection. Therefore, you will need to determine whether or not nonstationarity is because of a deterministic or a stochastic pattern earlier than making use of the right transformations.
On this put up, I illustrate three instructions that implement exams for the presence of a unit root utilizing simulated information.
Stochastic pattern
A easy instance of a course of with stochastic pattern is a random stroll.
Random stroll
Contemplate the next first-order autoregressive (AR) course of
start{equation}
label{rw}
y_t = y_{t-1} + epsilon_t tag{1}
finish{equation}
the place (y_t) is the dependent variable. The error time period, (epsilon_t), is unbiased and identically distributed with imply 0 and variance (sigma^2).
If the method begins from an preliminary worth (y_0 = 0), then (y_t) may be expressed as
[
y_t = sum_{i=1}^t epsilon_i
]
the place (sum_{i=1}^t epsilon_i) is the stochastic pattern part. The imply and variance of (y_t) are (E(y_t) = 0) and (mbox{var}(y_t) = tsigma^2). The imply is fixed whereas the variance will increase over time (t).
Random stroll with drift
Including a continuing time period to a random stroll course of yields a random stroll with drift expressed as
start{equation}
label{rwwd}
y_t = alpha + y_{t-1} + epsilon_t tag{2}
finish{equation}
the place (alpha) is the fixed time period. If the method begins from an preliminary worth (y_0=0), then (y_t) may be expressed as
[
y_t = alpha t + sum_{i=1}^t epsilon_i
]
which is now the sum of a linear deterministic part ((alpha t)) and a stochastic part. The imply and variance of (y_t) are (E(y_t) = alpha t) and (mbox{var}(y_t) = tsigma^2). Each the imply and the variance improve over time (t). Discover that if the worth of (alpha) is near zero, then a random stroll appears to be like much like a random stroll with drift.
Deterministic pattern
Contemplate the next mannequin with a linear deterministic time pattern,
[
y_t = alpha + delta t + phi y_{t-1} + epsilon_t
]
the place (delta) is a coefficient on the time index (t) and (|phi|<1) is the AR parameter. Discover {that a} random stroll with drift can be much like a linear deterministic time pattern mannequin, besides that the previous additionally accommodates a stochastic pattern along with the deterministic pattern.
Plots of nonstationary processes
First, I generate simulated information from a random stroll mannequin and a random stroll with a drift time period of 0.1 and plot the graph under. The code for producing the info and plots are supplied within the Appendix part.
As seen within the graph above, there isn’t a clear pattern, and the pink line seems to be shifted by a optimistic fixed time period from the blue line. If the collection are graphed individually, it’s unimaginable to differentiate whether or not the collection are generated from a random stroll or a random stroll with drift. Nonetheless, as a result of each the collection comprise a stochastic pattern, we will nonetheless apply differencing to realize a stationary collection.
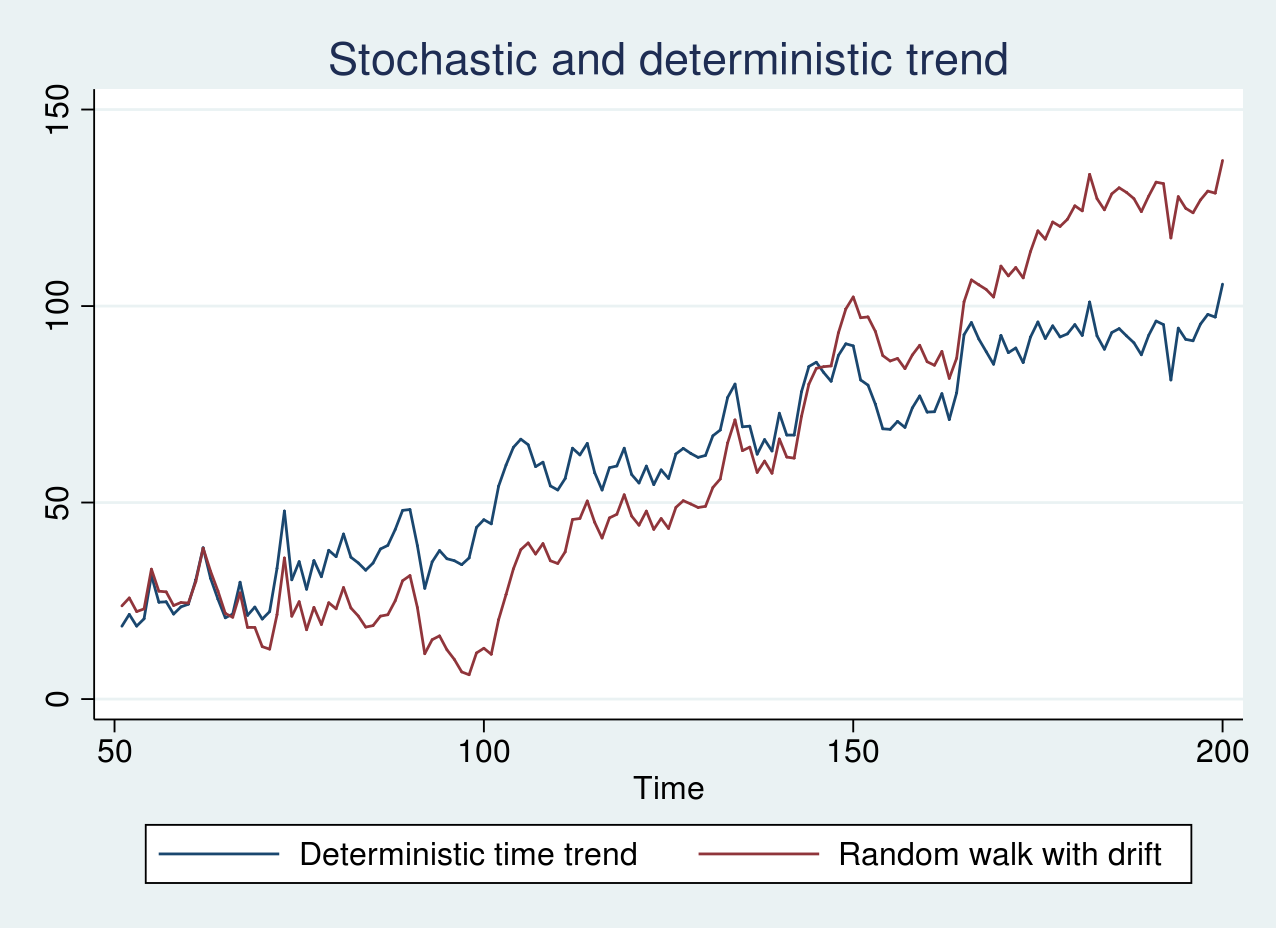
Equally, I generate simulated information from a random stroll with a drift time period of 1 and a deterministic time pattern mannequin and plot the graph under.
As seen within the graph above, the 2 collection look remarkably related. The blue line shows an erratic sample round a always growing pattern line. The stochastic pattern within the pink line, nonetheless, will increase slowly to start with of the pattern and quickly towards the top of the pattern. On this case, it’s essential to use the right transformation as talked about earlier.
Unit-root exams
Unit-root exams assume the null speculation that the true course of is a random stroll (1) or a random stroll with a drift (2). Contemplate the next AR(1) mannequin
[
y_t = phi y_{t-1} + epsilon_t
]
the place (epsilon_t) is unbiased and identically distributed with (N(0,sigma^2)) distribution. The null speculation corresponds to (phi=1), whereas the choice is (|phi|<1).
If (phi) is certainly 1, because the pattern measurement will increase, the OLS estimator ((hat{phi})) converges to the true worth of 1 at a quicker charge than it could if the method was stationary. Nonetheless, the asymptotic distribution of (hat{phi}) is nonstandard, and the standard (t) exams turn into invalid.
Moreover, relying on whether or not deterministic phrases comparable to constants and time tendencies are included within the regression results in totally different asymptotic distributions for the take a look at statistic. This underscores the significance of clearly specifying the null in addition to the choice hypotheses whereas performing these exams.
Augmented Dickey–Fuller take a look at
Beneath the null speculation, the true course of is both a random stroll or a random stroll with drift. The Dickey–Fuller take a look at includes becoming the mannequin
start{equation}
label{df}
y_t = alpha + delta t + phi y_{t-1} + epsilon_t tag{3}
finish{equation}
The null speculation corresponds to (phi=1). Estimating the parameters of (3) by OLS could fail to account for residual serial correlation. The augmented Dickey–Fuller (ADF) take a look at addresses this by augmenting (3) by (ok) variety of lagged variations of the dependent variable. Extra particularly, it transforms (3) in distinction type as
start{equation}
label{adf}
Delta y_t = alpha + delta t + beta y_{t-1} + sum_{i=1}^ok gamma_i Delta y_{t-i} + epsilon_t tag{4}
finish{equation}
and exams whether or not (beta=0). Be aware that (4) is in a normal type and we will prohibit (alpha) or (delta) or each to zero for regression specs that result in totally different distributions of the take a look at statistic. Hamilton (1994, ch. 17) lists the distribution of the take a look at statistic for 4 attainable instances.
I start by testing for a unit root within the collection yrwd2 and yt, which correspond to information from a random stroll with a drift time period of 1 and a linear deterministic time pattern mannequin, respectively. I take advantage of dfuller to carry out an ADF take a look at. The null speculation I’m involved in is that yrwd2 is a random stroll course of with a attainable drift, whereas the choice speculation posits that yrwd2 is stationary round a linear time pattern. Therefore, I take advantage of the choice pattern to regulate for a linear time pattern in (4).
. dfuller yrwd2, pattern
Dickey-Fuller take a look at for unit root Variety of obs = 149
---------- Interpolated Dickey-Fuller ---------
Take a look at 1% Crucial 5% Crucial 10% Crucial
Statistic Worth Worth Worth
----------------------------------------------------------------------------
Z(t) -2.664 -4.024 -3.443 -3.143
----------------------------------------------------------------------------
MacKinnon approximate p-value for Z(t) = 0.2511
As anticipated, we fail to reject the null speculation of a random stroll with a attainable drift in yrwd2. Equally, I take a look at the presence of a unit root within the yt collection.
. dfuller yt, pattern
Dickey-Fuller take a look at for unit root Variety of obs = 149
---------- Interpolated Dickey-Fuller ---------
Take a look at 1% Crucial 5% Crucial 10% Crucial
Statistic Worth Worth Worth
----------------------------------------------------------------------------
Z(t) -5.328 -4.024 -3.443 -3.143
----------------------------------------------------------------------------
MacKinnon approximate p-value for Z(t) = 0.0000
On this case, we reject the null speculation of a random stroll with drift.
Phillips–Perron take a look at
The exams developed in Phillips (1987) and Phillips and Perron (1988) modify the take a look at statistics to account for the potential serial correlation and heteroskedasticity within the residuals. As within the Dickey–Fuller take a look at, a regression mannequin as in (3) is match with OLS. The asymptotic distribution of the take a look at statistics and demanding values is identical as within the ADF take a look at.
pperron performs a PP take a look at in Stata and has the same syntax as dfuller. Utilizing pperron to check for a unit root in yrwd2 and yt yields the same conclusion because the ADF take a look at (output not proven right here).
GLS detrended augmented Dickey–Fuller take a look at
The GLS–ADF take a look at proposed by Elliott et al. (1996) is much like the ADF take a look at. Nonetheless, previous to becoming the mannequin in (4), one first transforms the precise collection through a generalized least-squares (GLS) regression. Elliott et al. (1996) present that this take a look at has higher energy than the ADF take a look at.
The null speculation is a random stroll with a attainable drift with two particular different hypotheses: the collection is stationary round a linear time pattern, or the collection is stationary round a attainable nonzero imply with no time pattern.
To check whether or not the yrwd2 collection is a random stroll with drift, I take advantage of dfgls with a most of 4 lags for the regression specification in (4).
. dfgls yrwd2, maxlag(4)
DF-GLS for yrwd2 Variety of obs = 145
DF-GLS tau 1% Crucial 5% Crucial 10% Crucial
[lags] Take a look at Statistic Worth Worth Worth
---------------------------------------------------------------------------
4 -1.404 -3.520 -2.930 -2.643
3 -1.420 -3.520 -2.942 -2.654
2 -1.638 -3.520 -2.953 -2.664
1 -1.644 -3.520 -2.963 -2.673
Decide Lag (Ng-Perron seq t) = 0 [use maxlag(0)]
Min SC = 3.31175 at lag 1 with RMSE 5.060941
Min MAIC = 3.295598 at lag 1 with RMSE 5.060941
Be aware that dfgls controls for a linear time pattern by default in contrast to the dfuller or pperron command. We fail to reject the null speculation of a random stroll with drift within the yrwd2 collection.
Lastly, I take a look at the null speculation that yt is a random stroll with drift utilizing dfgls with a most of 4 lags.
. dfgls yt, maxlag(4)
DF-GLS for yt Variety of obs = 145
DF-GLS tau 1% Crucial 5% Crucial 10% Crucial
[lags] Take a look at Statistic Worth Worth Worth
---------------------------------------------------------------------------
4 -4.013 -3.520 -2.930 -2.643
3 -4.154 -3.520 -2.942 -2.654
2 -4.848 -3.520 -2.953 -2.664
1 -4.844 -3.520 -2.963 -2.673
Decide Lag (Ng-Perron seq t) = 0 [use maxlag(0)]
Min SC = 3.302146 at lag 1 with RMSE 5.036697
Min MAIC = 3.638026 at lag 1 with RMSE 5.036697
As anticipated, we reject the null speculation of a random stroll with drift within the yt collection.
Conclusion
On this put up, I mentioned nonstationary processes arising due to a stochastic pattern, a deterministic time pattern, or a mixture of each. I illustrated the dfuller, pperron, and dfgls instructions for testing the presence of a unit root utilizing simulated information.
Appendix
The code for producing information from a random stroll, random stroll with drift, and linear deterministic pattern fashions is supplied under.
clear all
set seed 2016
native T = 200
set obs `T'
gen time = _n
label var time "Time"
tsset time
gen eps = rnormal(0,5)
/*Random stroll*/
gen yrw = eps in 1
change yrw = l.yrw + eps in 2/l
/*Random stroll with drift*/
gen yrwd1 = 0.1 + eps in 1
change yrwd1 = 0.1 + l.yrwd1 + eps in 2/l
/*Random stroll with drift*/
gen yrwd2 = 1 + eps in 1
change yrwd2 = 1 + l.yrwd2 + eps in 2/l
/*Stationary round a time pattern mannequin*/
gen yt = 0.5 + 0.1*time + eps in 1
change yt = 0.5 + 0.1*time +0.8*l.yt+ eps in 2/l
drop in 1/50
tsline yrw yrwd1, title("Stochastic pattern") ///
legend(label(1 "Random stroll") ///
label(2 "Random stroll with drift"))
tsline yt yrwd2, ///
legend(label(1 "Deterministic time pattern") ///
label(2 "Random stroll with drift")) ///
title("Stochastic and deterministic pattern")
Traces 1–4 clear the present Stata session, set the seed for the random quantity generator, outline a neighborhood macro T because the variety of observations, and set it to 200. Traces 5–7 generate the time variable and declare it as a time collection. Line 8 generates a zero imply random regular error with customary deviation 5. Traces 10–12 generate information from a random stroll mannequin and retailer them within the variable yrw. Traces 14–16 generate information from a random stroll with a drift of 0.1 and retailer them within the variable yrwd1. Traces 18–20 generate information from a random stroll with a drift of 1 and retailer within the variable yrwd2. Traces 22–24 generate information from a deterministic time pattern mannequin and retailer them within the variable yt. Line 25 drops the primary 50 observations as burn-in. Traces 27–33 plot the time collection.
References
Elliott, G. R., T. J. Rothenberg, and J. H. Inventory. 1996. Environment friendly exams for an autoregressive unit root. Econometrica 64: 813–836.
Hamilton, J. D. 1994. Time Collection Evaluation. Princeton: Princeton College Press.
Phillips, P. C. B. 1987. Time collection regression with a unit root. Econometrica 55: 277–301.
Phillips, P. C. B., and P. Perron. 1988. Testing for a unit root in time collection regression. Biometrika 75: 335–346.