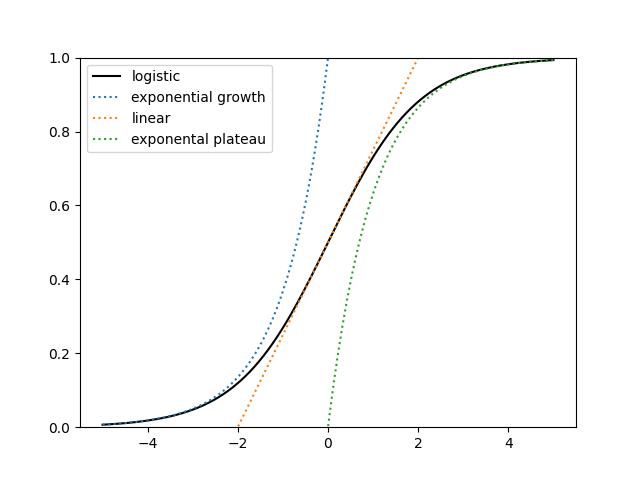
A logistic curve, generally referred to as an S curve, seems completely different in several areas. Just like the proverbial blind males feeling completely different elements of an elephant, individuals taking a look at completely different segments of the curve might come to very completely different impressions of the total image.
It’s naive to have a look at the left finish and assume the curve will develop exponentially ceaselessly, even when the info are statistically indistinguishable from exponential development.
A barely much less naive method is to have a look at the left finish, assume logistic development, and attempt to infer the parameters of the logistic curve. Within the picture above, you could possibly forecast the asymptotic worth when you have knowledge as much as time t = 2, however it might be hopeless to take action with solely knowledge as much as time t = −2. (This publish was motivated by seeing somebody attempting to extrapolate a logistic curve from simply its left tail.)
Suppose with absolute certainty that your knowledge have the shape
the place ε is a few small quantity of measurement error. The world just isn’t obligated comply with a easy mathematical mannequin, or any mathematical mannequin for that matter, however for this publish we’ll assume that for some inexplicable cause the longer term follows a logistic curve; the one query is what the parameters are.
Moreover, we solely care about becoming the a parameter. That’s, we solely need to predict the asymptotic worth of the curve. That is simpler than attempting to suit the b or c parameters.
Simulation experiment
I generated 16 random t values between −5 and −2, plugged them into the logistic perform with parameters a = 1, b = 1, and c = 0, then added Gaussian noise with normal deviation 0.05.
My intention was to do that 1000 occasions and report the vary of fitted values for a. Nonetheless, the software program I used to be utilizing (scipy.optimize.curve_fit) did not converge. As a substitute it returned the next error message.
RuntimeError: Optimum parameters not discovered: Variety of calls to perform has reached maxfev = 800.
If you see a message like that, your first response might be to tweak the code in order that it converges. Typically that’s the proper factor to do, however usually such numerical difficulties try to inform you that you just’re fixing the fallacious drawback.
Once I generated factors between −5 and 0, the curve_fit algorithm nonetheless did not converge.
Once I generated factors between −5 and a pair of, the becoming algorithm converged. The vary of a values was from 0.8254 to 1.6965.
Once I generated factors between −5 and three, the vary of a values was from 0.9039 to 1.1815.
Growing the variety of generated factors didn’t change whether or not the curve becoming methodology converge, although it did lead to a smaller vary of fitted parameter values when it did converge.
I stated we’re solely occupied with becoming the a parameter. I regarded on the ranges of the opposite parameters as effectively, and as anticipated, they’d a wider vary of values.
So in abstract, becoming a logistic curve with knowledge solely on the left aspect of the curve, to the left of the inflection level within the center, might fully fail or provide you with outcomes with huge error estimates. And it’s higher to have a couple of factors unfold out via the area of the perform than to have a lot of factors solely on one finish.