Deep studying fashions are based mostly on activation capabilities that present non-linearity and allow networks to be taught sophisticated patterns. This text will talk about the Softplus activation perform, what it’s, and the way it may be utilized in PyTorch. Softplus could be stated to be a clean type of the favored ReLU activation, that mitigates the drawbacks of ReLU however introduces its personal drawbacks. We’ll talk about what Softplus is, its mathematical components, its comparability with ReLU, what its benefits and limitations are and take a stroll by means of some PyTorch code using it.
What’s Softplus Activation Operate?
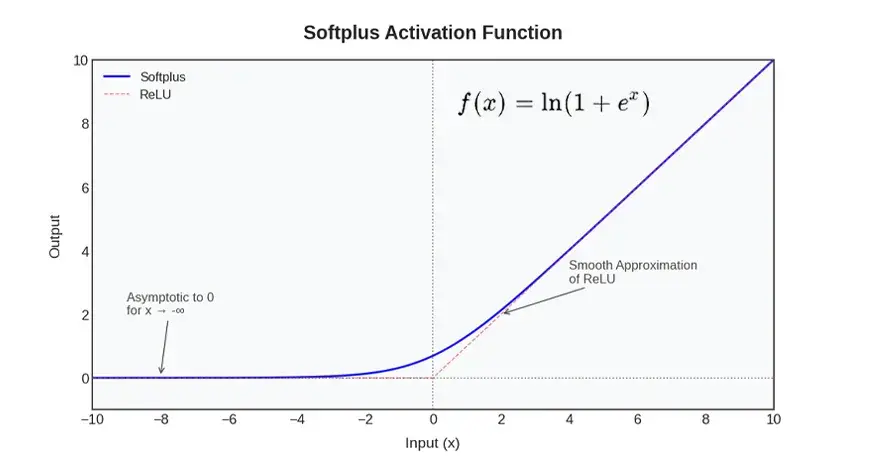
Softplus activation perform is a non-linear perform of neural networks and is characterised by a clean approximation of the ReLU perform. In simpler phrases, Softplus acts like ReLU in instances when the optimistic or detrimental enter may be very giant, however a pointy nook on the zero level is absent. As a replacement, it rises easily and yields a marginal optimistic output to detrimental inputs as an alternative of a agency zero. This steady and differentiable habits implies that Softplus is steady and differentiable all over the place in distinction to ReLU which is discontinuous (with a pointy change of slope) at x = 0.
Why is Softplus used?
Softplus is chosen by builders that choose a extra handy activation that provides. non-zero gradients additionally the place ReLU would in any other case be inactive. Gradient-based optimization could be spared main disruptions attributable to the smoothness of Softplus (the gradient is shifting easily as an alternative of stepping). It additionally inherently clips outputs (as ReLU does) but the clipping is to not zero. In abstract, Softplus is the softer model of ReLU: it’s ReLU-like when the worth is giant however is healthier round zero and is good and clean.
Softplus Mathematical Formulation
The Softplus is mathematically outlined to be:
When x is giant, ex may be very giant and due to this fact, ln(1 + ex) is similar to ln(ex), equal to x. It implies that Softplus is almost linear at giant inputs, equivalent to ReLU.
When x is giant and detrimental, ex may be very small, thus ln(1 + ex) is almost ln(1), and that is 0. The values produced by Softplus are near zero however by no means zero. To tackle a worth that’s zero, x should method detrimental infinity.
One other factor that’s useful is that the spinoff of Softplus is the sigmoid. The spinoff of ln(1 + ex) is:
ex / (1 + ex)
That is the very sigmoid of x. It implies that at any second, the slope of Softplus is sigmoid(x), that’s, it has a non-zero gradient all over the place and is clean. This renders Softplus helpful in gradient-based studying because it doesn’t have flat areas the place the gradients vanish.
Utilizing Softplus in PyTorch
PyTorch supplies the activation Softplus as a local activation and thus could be simply used like ReLU or some other activation. An instance of two easy ones is given under. The previous makes use of Softplus on a small variety of take a look at values, and the latter demonstrates the best way to insert Softplus right into a small neural community.
Softplus on Pattern Inputs
The snippet under applies nn.Softplus to a small tensor so you may see the way it behaves with detrimental, zero, and optimistic inputs.
import torch
import torch.nn as nn
# Create the Softplus activation
softplus = nn.Softplus() # default beta=1, threshold=20
# Pattern inputs
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
y = softplus(x)
print("Enter:", x.tolist())
print("Softplus output:", y.tolist())
What this reveals:
- At x = -2 and x = -1, the worth of Softplus is small optimistic values quite than 0.
- The output is roughly 0.6931 at x =0, i.e. ln(2)
- In case of optimistic inputs equivalent to 1 or 2, the outcomes are somewhat larger than the inputs since Softplus smoothes the curve. Softplus is approaching x because it will increase.
The Softplus of PyTorch is represented by the components ln(1 + exp(betax)). Its inner threshold worth of 20 is to stop a numerical overflow. Softplus is linear in giant betax, that means that in that case of PyTorch merely returns x.
Utilizing Softplus in a Neural Community
Right here is an easy PyTorch community that makes use of Softplus because the activation for its hidden layer.
import torch
import torch.nn as nn
class SimpleNet(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
tremendous(SimpleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.activation = nn.Softplus()
self.fc2 = nn.Linear(hidden_size, output_size)
def ahead(self, x):
x = self.fc1(x)
x = self.activation(x) # apply Softplus
x = self.fc2(x)
return x
# Create the mannequin
mannequin = SimpleNet(input_size=4, hidden_size=3, output_size=1)
print(mannequin)
Passing an enter by means of the mannequin works as ordinary:
x_input = torch.randn(2, 4) # batch of two samples
y_output = mannequin(x_input)
print("Enter:n", x_input)
print("Output:n", y_output)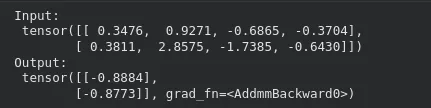
On this association, Softplus activation is used in order that the values exited within the first layer to the second layer are non-negative. The alternative of Softplus by an current mannequin could not want some other structural variation. It’s only essential to do not forget that Softplus may be somewhat slower in coaching and require extra computation than ReLU.
The ultimate layer might also be applied with Softplus when there are optimistic values {that a} mannequin ought to generate as outputs, e.g. scale parameters or optimistic regression aims.
Softplus vs ReLU: Comparability Desk
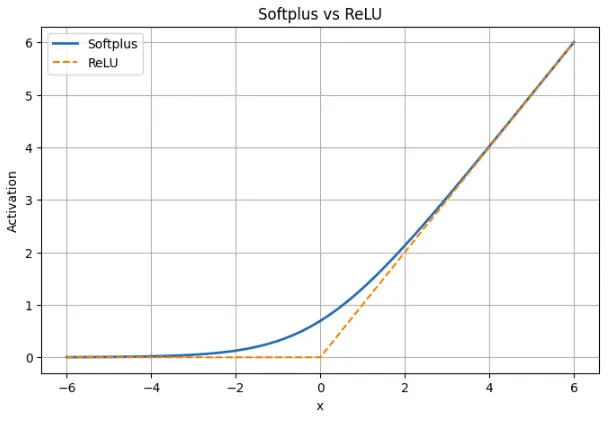
| Side | Softplus | ReLU |
|---|---|---|
| Definition | f(x) = ln(1 + ex) | f(x) = max(0, x) |
| Form | Easy transition throughout all x | Sharp kink at x = 0 |
| Habits for x < 0 | Small optimistic output; by no means reaches zero | Output is precisely zero |
| Instance at x = -2 | Softplus ≈ 0.13 | ReLU = 0 |
| Close to x = 0 | Easy and differentiable; worth ≈ 0.693 | Not differentiable at 0 |
| Habits for x > 0 | Virtually linear, carefully matches ReLU | Linear with slope 1 |
| Instance at x = 5 | Softplus ≈ 5.0067 | ReLU = 5 |
| Gradient | At all times non-zero; spinoff is sigmoid(x) | Zero for x < 0, undefined at 0 |
| Danger of useless neurons | None | Attainable for detrimental inputs |
| Sparsity | Doesn’t produce actual zeros | Produces true zeros |
| Coaching impact | Secure gradient circulation, smoother updates | Easy however can cease studying for some neurons |
An analog of ReLU is softplus. It’s ReLU with very giant optimistic or detrimental inputs however with the nook at zero eliminated. This prevents useless neurons because the gradient doesn’t go to a zero. This comes on the value that Softplus doesn’t generate true zeros that means that it’s not as sparse as ReLU. Softplus supplies extra snug coaching dynamics within the observe, however ReLU remains to be used as a result of it’s sooner and easier.
Advantages of Utilizing Softplus
Softplus has some sensible advantages that render it to be helpful in some fashions.
- All over the place clean and differentiable
There aren’t any sharp corners in Softplus. It’s fully differentiable to each enter. This assists in sustaining gradients which will find yourself making optimization somewhat simpler because the loss varies slower.
- Avoids useless neurons
ReLU can forestall updating when a neuron repeatedly will get detrimental enter, because the gradient can be zero. Softplus doesn’t give the precise zero worth on detrimental numbers and thus all of the neurons stay partially energetic and are up to date on the gradient.
- Reacts extra favorably to detrimental inputs
Softplus doesn’t throw out the detrimental inputs by producing a zero worth as ReLU does however quite generates a small optimistic worth. This permits the mannequin to retain part of data of detrimental alerts quite than dropping all of it.
Concisely, Softplus maintains gradients flowing, prevents useless neurons and presents clean habits for use in some architectures or duties the place continuity is essential.
Limitations and Commerce-offs of Softplus
There are additionally disadvantages of Softplus that limit the frequency of its utilization.
- Dearer to compute
Softplus makes use of exponential and logarithmic operations which might be slower than the easy max(0, x) of ReLU. This extra overhead could be visibly felt on giant fashions as a result of ReLU is extraordinarily optimized on most {hardware}.
- No true sparsity
ReLU generates good zeroes on detrimental examples, which may save computing time and infrequently help in regularization. Softplus doesn’t give an actual zero and therefore all of the neurons are at all times not inactive. This eliminates the chance of useless neurons in addition to the effectivity benefits of sparse activations.
- Step by step decelerate the convergence of deep networks
ReLU is usually used to coach deep fashions. It has a pointy cutoff and linear optimistic area which may pressure studying. Softplus is smoother and may need sluggish updates notably in very deep networks the place the distinction between layers is small.
To summarize, Softplus has good mathematical properties and avoids points like useless neurons, however these advantages don’t at all times translate to higher ends in deep networks. It’s best utilized in instances the place smoothness or optimistic outputs are essential, quite than as a common alternative for ReLU.
Conclusion
Softplus supplies clean, mushy options of ReLU to the neural networks. It learns gradients, doesn’t kill neurons and is absolutely differentiable all through the inputs. It’s like ReLU at giant values, however at zero, behaves extra like a relentless than ReLU as a result of it produces non-zero output and slope. In the meantime, it’s related to trade-offs. It is usually slower to compute; it additionally doesn’t generate actual zeros and should not speed up studying in deep networks as rapidly as ReLU. Softplus is simpler in fashions, the place gradients are clean or the place optimistic outputs are necessary. In most different situations, it’s a helpful various to a default alternative of ReLU.
Continuously Requested Questions
A. Softplus prevents useless neurons by maintaining gradients non-zero for all inputs, providing a clean various to ReLU whereas nonetheless behaving equally for big optimistic values.
A. It’s a good selection when your mannequin advantages from clean gradients or should output strictly optimistic values, like scale parameters or sure regression targets.
A. It’s slower to compute than ReLU, doesn’t create sparse activations, and may result in barely slower convergence in deep networks.
Login to proceed studying and luxuriate in expert-curated content material.