November 20, 2020
Neural tangent kernels are a great tool for understanding neural community coaching and implicit regularization in gradient descent. However it’s not the best idea to wrap your head round. The paper that I discovered to have been most helpful for me to develop an understanding is that this one:
On this submit I’ll illustrate the idea of neural tangent kernels via a easy 1D regression instance. Please be at liberty to peruse the google colab pocket book I used to make these plots.
Instance 1: Warming up
Let’s begin from a really boring case start with. To illustrate we now have a perform outlined over integers between -10 and 20. We parametrize our perform as a look-up desk, that’s the worth of the perform $f(i)$ at every integer $i$ is described by a separate parameter $theta_i = f(i)$. I am initializing the parameters of this perform as $theta_i = 3i+2$. The perform is proven by the black dots beneath:
Now, let’s take into account what occurs if we observe a brand new datapoint, $(x, y) =(10, 50)$, proven by the blue cross. We will take a gradient descent step updating $theta$. To illustrate we use the squared error loss perform $(f(10; theta) – 50)^2$ and a studying price $eta=0.1$. As a result of the perform’s worth at $x=10$ solely will depend on one of many parameter $theta_10$, solely this parameter shall be up to date. The remainder of the parameters, and subsequently the remainder of the perform values stay unchanged. The crimson arrows illustrate the best way perform values transfer in a single gradient descent step: Most values do not transfer in any respect, solely considered one of them strikes nearer to the noticed information. Therefore just one seen crimson arrow.
Nonetheless, in machine studying we hardly ever parametrize features as lookup tables of particular person perform values. This parametrization is fairly ineffective because it would not will let you interpolate not to mention extrapolate to unseen information. Let’s have a look at what occurs in a extra acquainted mannequin: linear regression.
Instance 2: Linear perform
Let’s now take into account the linear perform $f(x, theta) = theta_1 x + theta_2$. I initialize the parameters to $theta_1=3$ and $theta_2=1$, so at initialisation, I’ve precisely the identical perform over integers as I had within the first instance. Let us take a look at what occurs to this perform as I replace $theta$ by performing single gradient descent step incorporating the remark $(x, y) =(10, 50)$ as earlier than. Once more, crimson arrows are present how perform values transfer:
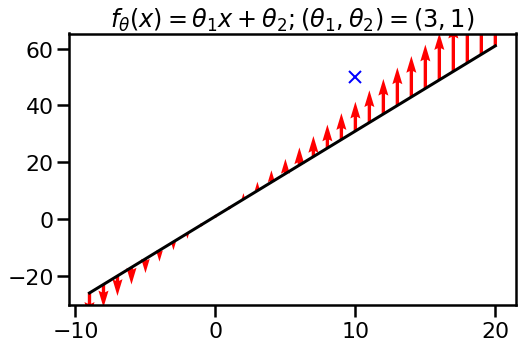
Whoa! What is going on on now? Since particular person perform values are now not independently parametrized, we will not transfer them independently. The mannequin binds them collectively via its world parameters $theta_1$ and $theta_2$. If we wish to transfer the perform nearer to the specified output $y=50$ at location $x=10$ the perform values elsewhere have to alter, too.
On this case, updating the perform with an remark at $x=10$ adjustments the perform worth far-off from the remark. It even adjustments the perform worth in the other way than what one would anticipate.. This may appear a bit bizarre, however that is actually how linear fashions work.
Now we now have somewhat little bit of background to begin speaking about this neural tangent kernel factor.
Meet the neural tangent kernel
Given a perform $f_theta(x)$ which is parametrized by $theta$, its neural tangent kernel $k_theta(x, x’)$ quantifies how a lot the perform’s worth at $x$ adjustments as we take an infinitesimally small gradient step in $theta$ incorporating a brand new remark at $x’$. One other approach of phrasing that is: $ok(x, x’)$ measures how delicate the perform worth at $x$ is to prediction errors at $x’$.
Within the plots earlier than, the scale of the crimson arrows at every location $x$ got by the next equation:
$$
eta tilde{ok}_theta(x, x’) = fleft(x, theta + eta frac{f_theta(x’)}{dtheta}proper) – f(x, theta)
$$
In neural community parlance, that is what is going on on: The loss perform tells me to extend the perform worth $f_theta(x’)$. I back-propagate this via the community to see what change in $theta$ do I’ve to make to attain this. Nonetheless, shifting $f_theta(x’)$ this manner additionally concurrently strikes $f_theta(x)$ at different areas $x neq x’$. $tilde{ok}_theta(x, x’)$ expresses by how a lot.
The neural kernel is mainly one thing just like the restrict of $tilde{ok}$ in because the stepsize turns into infinitesimally small. Particularly:
$$
ok(x, x’) = lim_{eta rightarrow 0} frac{fleft(x, theta + eta frac{df_theta(x’)}{dtheta}proper) – f(x, theta)}{eta}
$$
Utilizing a 1st order Taylor enlargement of $f_theta(x)$, it’s doable to indicate that
$$
k_theta(x, x’) = leftlangle frac{df_theta(x)}{dtheta} , frac{f_theta(x’)}{dtheta} rightrangle
$$
As homework for you: discover $ok(x, x’)$ and/or $tilde{ok}(x, x’)$ for a set $eta$ within the linear mannequin within the pervious instance. Is it linear? Is it one thing else?
Word that this can be a totally different derivation from what’s within the paper (which begins from steady differential equation model of gradient descent).
Now, I am going to return to the examples as an example two extra necessary property of this kernel: sensitivity to parametrization, and adjustments throughout coaching.
Instance 3: Reparametrized linear mannequin
It is well-known that neural networks could be repararmetized in ways in which do not change the precise output of the perform, however which can result in variations in how optimization works. Batchnorm is a well known instance of this. Can we see the impact of reparametrization within the neural tangent kernel? Sure we are able to. Let us take a look at what occurs if I reparametrize the linear perform I used within the second instance as:
$$
f_theta(x) = theta_1 x + colour{blue}{10cdot}theta_2
$$
however now with parameters $theta_1=3, theta_2=colour{blue}{0.1}$. I highlighted in blue what modified. The perform itself, at initialization is identical since $10 * 0.1 = 1$. The perform class is identical, too, as I can nonetheless implement arbitrary linear features. Nonetheless, after we have a look at the impact of a single gradient step, we see that the perform adjustments otherwise when gradient descent is carried out on this parametrisation.
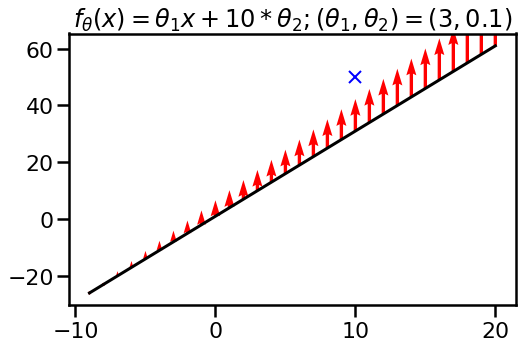
On this parametization, it grew to become simpler for gradient descent to push the entire perform up by a continuing, whereas within the earlier parametrisation it determined to alter the slope. What this demonstrates is that the neural tangent kernel $k_theta(x, x’)$ is delicate to reparametrization.
Instance 4: tiny radial foundation perform community
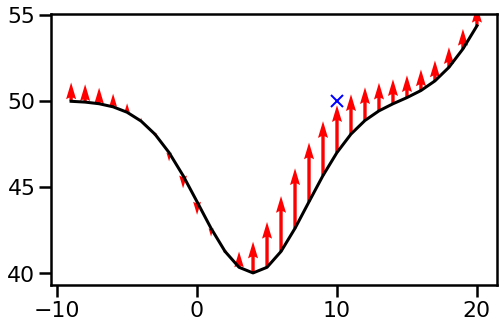
Whereas the linear fashions could also be good illustration, let’s take a look at what $k_theta(x, x’)$ appears to be like like in a nonlinear mannequin. Right here, I am going to take into account a mannequin with two squared exponential foundation features:
$$
f_theta(x) = theta_1 expleft(-frac{(x – theta_2)^2}{30}proper) + theta_3 expleft(-frac{(x – theta_4)^2}{30}proper) + theta_5,
$$
with preliminary parameter values $(theta_1, theta_2, theta_3, theta_4, theta_5) = (4.0, -10.0, 25.0, 10.0, 50.0)$. These are chosen considerably arbitrarily and to make the outcome visually interesting:
We are able to visualise the perform $tilde{ok}_theta(x, 10)$ immediately, slightly than plotting it on prime the perform. Right here I additionally normalize it by dividing by $tilde{ok}_theta(10, 10)$.
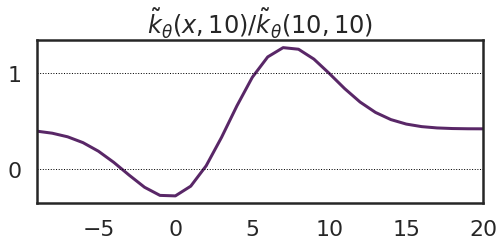
What we are able to see is that this begins to look a bit like a kernel perform in that it has greater values close to $10$ and reduces as you go farther away. Nonetheless, a couple of issues are price noting: the utmost of this kernel perform shouldn’t be at $x=1o$, however at $x=7$. It means, that the perform worth $f(7)$ adjustments extra in response to an remark at $x’=10$ than the worth $f(10)$. Secondly, there are some damaging values. On this case the earlier determine offers a visible reason why: we are able to enhance the perform worth at $x=10$ by pushing the valley centred at $theta_1=4$ away from it, to the left. This parameter change in flip decreases perform values on the left-hand wall of the valley. Third, the kernel perform converges to a constructive fixed at its tails – that is due to the offset $theta_5$.
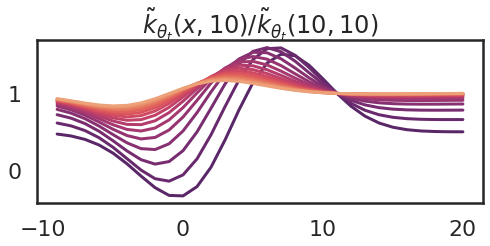
Instance 5: Modifications as we prepare
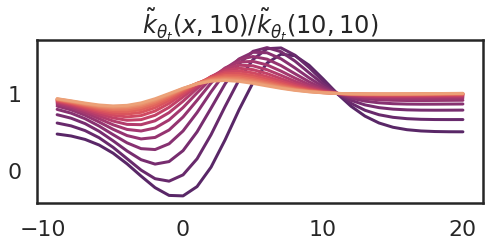
Now I’ll illustrate one other necessary property of the neural tangent kernel: typically, the kernel will depend on the parameter worth $theta$, and subsequently it adjustments because the mannequin is skilled. Right here I present what occurs to the kernel as I take 15 gradient ascent steps making an attempt to extend $f(10)$. The purple curve is the one I had at initialization (above), and the orange ones present the kernel on the final gradient step.
The corresponding adjustments to the perform $f_theta_t$ adjustments are proven beneath:
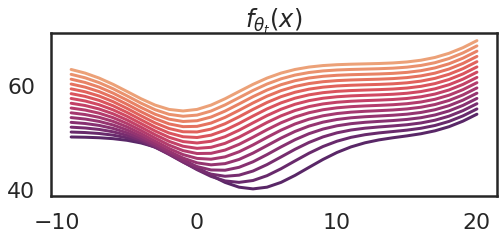
So we are able to see that because the parameter adjustments, the kernel additionally adjustments. The kernel turns into flatter. An evidence of that is that ultimately we attain a area of parameter area, the place $theta_4$ adjustments the quickest.
Why is that this attention-grabbing?
It seems the neural tangent kernel turns into notably helpful when learning studying dynamics in infinitely broad feed-forward neural networks. Why? As a result of on this restrict, two issues occur:
- First: if we initialize $theta_0$ randomly from appropiately chosen distributions, the preliminary NTK of the community $k_{theta_0}$ approaches a deterministic kernel because the width will increase. This implies, that at initialization, $k_{theta_0}$ would not actually depend upon $theta_0$ however is a set kernel impartial of the particular initialization.
- Second: within the infinite restrict the kernel $k_{theta_t}$ stays fixed over time as we optimise $theta_t$. This removes the parameter dependence throughout coaching.
These two info put collectively indicate that gradient descent within the infinitely broad and infinitesimally small studying price restrict could be understood as a fairly easy algorithm referred to as kernel gradient descent with a set kernel perform that relies upon solely on the structure (variety of layers, activations, and so forth).
These outcomes, taken along with an older identified outcome by Neal, (1994), permits us to characterise the chance distribution of minima that gradient descent converges to on this infinite restrict as a Gaussian course of. For particulars, see the paper talked about above.
Do not combine your kernels
There are two considerably associated units of outcomes each involving infinitely broad neural netwoks and kernel features, so I simply needed to make clear the distinction between them:
- the older, well-known outcome by Neal, (1994), later prolonged by others, is that the distribution of $f_theta$ beneath random initialization of $theta$ converges to a Gaussian course of. This Gaussian course of has a kernel or covariance perform which isn’t, typically, the identical because the neural tangent kernel. This previous outcome would not say something about gradient descent, and is usually used to encourage the usage of Gaussian process-based Bayesian strategies.
- the brand new, NTK, result’s that the evolution of $f_{theta_t}$ throughout gradient descent coaching could be described by way of a kernel, the neural tangent kernel, and that within the infinite restrict this kernel stays fixed throughout coaching and is deterministic at initialization. Utilizing this outcome, it’s doable to indicate that in some instances the distribution of $f_{theta_t}$ is a Gaussian course of at each timestep $t$, not simply at initialization. This outcome additionally permits us to establish the Gaussian course of which describes the restrict as $t rightarrow infty$. This limiting Gaussian course of nevertheless shouldn’t be the identical because the posterior Gaussian course of which Neal and others would calculate on the idea of the primary outcome.
So I hope this submit helps a bit by constructing some instinct about what the neural tangent kernel is. Should you’re , take a look at the easy colab pocket book I used for these illustrations.