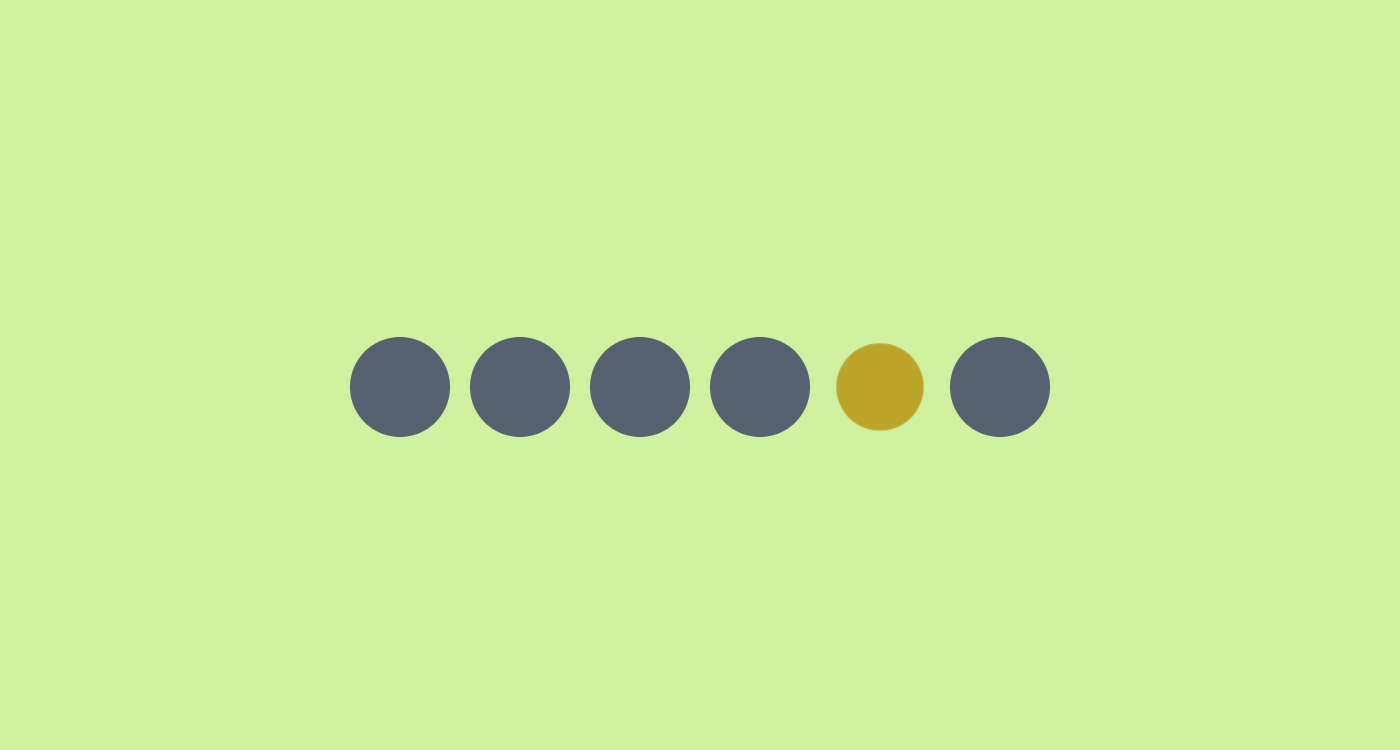Sequential linear() Animation With N Components

Let’s suppose you may have N parts with the identical animation that ought to animate sequentially. The primary one, then the second, and so forth till we attain the final one, then we loop again to the start. I’m certain you understand what I’m speaking about, and also you additionally know that it’s difficult to get such an impact. You have to outline advanced keyframes, calculate delays, make it work for a selected variety of objects, and many others.

Inform you what: with fashionable CSS, we are able to simply obtain this utilizing a number of strains of code, and it really works for any variety of objects!

The next demo is at the moment restricted to Chrome and Edge, however will work in different browsers because the sibling-index() and sibling-count() capabilities achieve broader assist. You’ll be able to observe Firefox assist in Ticket #1953973 and WebKit’s place in Situation #471.

Within the above demo, the weather are animated sequentially and the keyframes are so simple as a single to body altering a component’s background coloration and scale:

@keyframes x {
  to {
    background: #F8CA00;
    scale: .8;
  }
}

You’ll be able to add or take away as many objects as you need and all the things will hold operating easily. Cool, proper? That impact is made potential with this unusual and complex-looking code:

.container > * {
  --_s: calc(100%*(sibling-index() - 1)/sibling-count());
  --_e: calc(100%*(sibling-index())/sibling-count());

  animation: 
    x calc(var(--d)*sibling-count()) infinite 
    linear(0, 0 var(--_s), 1, 0 var(--_e), 0);
}

It’s a bit scary and unreadable, however I’ll dissect it with you to grasp the logic behind it.

The CSS linear() operate

When working with animations, we are able to outline timing capabilities (additionally referred to as easing capabilities). We will use predefined key phrase values — corresponding to linear, ease, ease-in, and many others. — or steps() to outline discrete animations. There’s additionally cubic-bezier().

However we have now a more moderen, extra highly effective operate we are able to add to that listing: linear().

From the specification:

A linear easing operate is an easing operate that interpolates linearly between its management factors. Every management level is a pair of numbers, associating an enter progress worth to an output progress worth.

animation-timing-function: linear creates a linear interpolation between two factors — the begin and finish of the animation — whereas the linear() operate permits us to outline as many factors as we would like and have a “linear” interpolation between two consecutive factors.

It’s a bit complicated at first look, however as soon as we begin working with it, issues turns into clearer. Let’s begin with the primary worth, which is nothing however an equal of the linear worth.

linear(0 0%, 1 100%)

Now we have two factors, and every level is outlined with two values (the “output” progress and “enter” progress). The “output” progress is the animation (i.e., what’s outlined throughout the keyframes) and the “enter” progress is the time.

Let’s contemplate the next code:

.field {
  animation: transfer 2s linear(0 0%, 1 100%);
}

@keyframes transfer {
  0%   {translate: 0px }
  100% {translate: 80px}
}

On this case, we would like 0 of the animation (translate: 0px) at t=0% (in different phrases, 0% of 2s, so 0s) and 1 of the animation (translate: 80px) at t=100% (which is 100% of 2s, so 2s). Between these factors, we do a linear interpolation.

As an alternative of percentages, we are able to use numbers, which implies that the next can be legitimate:

linear(0 0, 1 1)

However I like to recommend you stick with the share notation to keep away from getting confused with the primary worth which is a quantity as properly. The 0% and 100% are implicit, so we are able to take away them and easily use the next:

linear(0, 1)

Let’s add a 3rd level:

linear(0, 1, 0)

As you’ll be able to see, I’m not defining any “enter” progress (the share values that characterize the time) as a result of they don’t seem to be necessary; nevertheless, introducing them is the very first thing to do to grasp what the operate is doing.

The primary worth is at all times at 0% and the final worth is at all times at 100%.

linear(0 0%, 1, 0 100%)

The worth can be 50% for the center level. When a management level is lacking its “enter” progress, we take the mid-value between two adjoining factors. In case you are accustomed to gradients, you’ll discover the identical logic applies to paint stops.

linear(0 0%, 1 50%, 0 100%)

Simpler to learn, proper? Are you able to clarify what it does? Take a couple of minutes to consider it earlier than persevering with.

Obtained it? I’m certain you probably did!

It breaks down like this:

1. We begin with translate: 0px at t=0s (0% of 2s).
2. Then we transfer to translate: 80px at t=1s (50% of 2s).
3. Then we get again to translate: 0px at t=2s (100% of 2s).

Many of the timing capabilities enable us to solely transfer ahead, however with linear() we are able to transfer in each instructions as many occasions as we would like. That’s what makes this operate so highly effective. With a “easy” keyframes you’ll be able to have a “advanced” animation.

I might have used the next keyframes to do the identical factor:

@keyframes transfer {
  0%, 100% { translate: 0px }
  50% { translate: 80px }
}

Nonetheless, I gained’t be capable of replace the share values on the fly if I desire a totally different animation. There isn’t a strategy to management keyframes utilizing CSS so I must outline new keyframes every time I want a brand new animation. However with linear(), I solely want one keyframes.

Within the demo under, all the weather are utilizing the identical keyframes and but have fully totally different animations!

Add a delay with linear()

Now that we all know extra about linear(), let’s transfer to the primary trick of our impact. Don’t overlook that the concept is to create a sequential animation with a sure quantity (N) of parts. Every factor must animate, then “wait” till all of the others are carried out with their animation to begin once more. That ready time might be seen as a delay.

The intuitive means to do that is the next:

@keyframes transfer {
  0%, 50% { translate: 0px }
  100% { translate: 80px }
}

We specify the identical worth at 0% and 50%; therefore nothing will occur between 0% and 50%. Now we have our delay, however as I mentioned beforehand, we gained’t be capable of management these percentages utilizing CSS. As an alternative, we are able to categorical the identical factor utilizing linear():

linear(0 0%, 0 50%, 1 100%)

The primary two management factors have the identical “output” progress. The primary one is at 0% of the time, and the second at 50% of the time, so nothing will “visually” occur within the first half of the animation. We created a delay with out having to replace the keyframes!

@keyframes transfer {
  0% { translate: 0px }
  100% { translate: 80px }
}

Let’s add one other level to get again to the preliminary state:

linear(0 0%, 0 50%, 1 75%, 0 100%)

Or just:

linear(0, 0 50%, 1, 0)

Cool, proper? We’re capable of create a posh animation with a easy set of keyframes. Not solely that, however we are able to simply regulate the configuration by tweaking the linear() operate. That is what we are going to do for every factor to get our sequential animation!

The complete animation

Let’s get again to our first animation and use the earlier linear() worth we did earlier than. We’ll begin with two parts.

Nothing stunning but. Each parts have the very same animation, in order that they animate the identical means on the similar time. Now, let’s replace the linear() operate for the primary factor to have the other impact: an animation within the first half, then a delay within the second half.

linear(0, 1, 0 50%, 0)

This actually inverts the earlier worth:

Tada! Now we have established a sequential animation with two parts! Are you beginning to see the concept? The purpose is to do the identical with any quantity (N) of parts. After all, we aren’t going to assign a special linear() worth for every factor — we are going to do it programmatically.

First, let’s draw a determine to grasp what we did for 2 parts.

When one factor is ready, the opposite one is animating. We will establish two ranges. Let’s think about the identical with three parts.

This time, we want three ranges. Every factor animates in a single vary and waits in two ranges. Do you see the sample? For N parts, we want N ranges, and the linear() operate can have the next syntax:

linear(0, 0 S, 1, 0 E, 0)

The begin and the finish are equal to 0, which is the preliminary state of the animation, then we have now an animation between S and E. A component will wait from 0% to S, animate from S to E, then wait once more from E to 100%. The animation time equals to 100%/N, which suggests E - S = 100%/N.

The primary factor begins its animation on the first vary (0 * 100%/N), the second factor on the second vary (1 * 100%/N), the third factor on the third vary (2 * 100%/N), and so forth. S is the same as:

S = (i - 1) * 100%/N

…the place i is the index of the factor.

Now, you could ask, how will we get the worth of N and i? The reply is so simple as utilizing the sibling-count()and sibling-index() capabilities! Once more, these are at the moment supported in Chromium browsers, however we are able to count on them to roll out in different browsers down the highway.

S = calc(100%*(sibling-index() - 1)/sibling-count())

And:

E = S + 100%/N
E = calc(100%*sibling-index()/sibling-count())

We write all this with some good CSS and we’re carried out!

.field {
  --d: .5s; /* animation period */
  --_s: calc(100%*(sibling-index() - 1)/sibling-count());
  --_e: calc(100%*(sibling-index())/sibling-count());

  animation: x calc(var(--d)*sibling-count()) infinite linear(0, 0 var(--_s), 1, 0 var(--_e), 0);
}
@keyframes x {
  to {
    background: #F8CA00;
    scale: .8;
  }
}

I used a variable (--d) to manage the period, nevertheless it’s not necessary. I needed to have the ability to management the period of time every factor takes to animate. That’s why I multiply it later by N.

Now all that’s left is to outline your animation. Add as many parts as you need, and watch the outcome. No extra advanced keyframes and magic values!

Observe: For unknown causes (in all probability a bug) you could register the variables with @property.

Extra variations

We will prolong the essential thought to create extra variations. For instance, as a substitute of getting to attend for a component to fully finish its animation, the subsequent one can already begin its personal.

This time, I’m defining N + 1 ranges, and every factor animates in two ranges. The primary factor will animate within the first and second vary, whereas the second factor will animate within the second and third vary; therefore an overlap of each animations within the second vary, and many others.

I can’t spend an excessive amount of time explaining this case as a result of it’s one instance amongst many we create, so I allow you to dissect the code as a small train. And right here is one other one so that you can examine as properly.

Conclusion

The linear() operate was primarily launched to create advanced easing corresponding to bounce and elastic, however mixed with different fashionable options, it unlocks a whole lot of prospects. By this text, we received a small overview of its potential. I mentioned “small” as a result of we are able to go additional and create much more advanced animations, so keep tuned for extra articles to come back!