Quantile regression fashions a quantile of the result as a operate of covariates. Utilized researchers use quantile regressions as a result of they permit the impact of a covariate to vary throughout conditional quantiles. For instance, one other yr of schooling might have a big impact on a low conditional quantile of revenue however a a lot smaller impact on a excessive conditional quantile of revenue. Additionally, one other pack-year of cigarettes might have a bigger impact on a low conditional quantile of bronchial effectiveness than on a excessive conditional quantile of bronchial effectiveness.
I exploit simulated information for instance what the conditional quantile capabilities estimated by quantile regression are and what the estimable covariate results are.
Simulated information to grasp conditional quantiles
Suppose that every quantity between 0 and 1 corresponds to the fortune of a person, or observational unit, within the inhabitants. In a way, every quantity between 0 and 1 specifies the rank of a person. For a given (x), a conditional quantile (Q(tau|x)) maps a rank (tauin[0,1]) to an final result (y). This mapping is basically an inverse of the conditional distribution operate. For every (x), a conditional distribution operate (F(y|x)) maps an final result (y) right into a chance that should be between 0 and 1.
I drew simulated information from a Weibull distribution for instance what conditional quantiles are. The graph beneath accommodates a scatterplot of the result (y) towards the covariate (x). I embrace plots of the conditional imply (y) given (x) (E[y|x]), the conditional 0.8 quantile of (y) given (x) (Q(0.8|x)), the conditional median of (y) given (x) (Q(0.5|x)), and the conditional 0.2 quantile of (y) given (x) (Q(0.2|x)).
The Q(0.8|x) curve plots the result (y) comparable to the rank of 0.8 for every (x). The Q(0.5|x) curve plots the result (y) comparable to the rank of 0.5 for every (x). The Q(0.2|x) curve plots the result (y) comparable to the rank of 0.2 for every (x). Q(0.8|x)>Q(0.5|x)>Q(0.2|x) for every (x) as a result of (0.8>0.5>0.2).
The conditional imply and the conditional quantiles curve upward as a result of I used a quadratic in (x) within the Weibull distribution of (y) given (x). The conditional imply is above the conditional median as a result of the Weibull distribution has a protracted, skinny proper tail.
Whereas the graph of the simulated information and the conditional quantiles supplies some instinct, some technical particulars present a deeper understanding. The practical kind for the distribution of (y) given (x) from which I drew the info is
start{equation}
label{F}tag{1}
F(y|x)=1 -expleft[-left(frac{y}{
beta_0 + beta_1 x + beta_2 x^2
}right)^{alpha}right]
finish{equation}
The quantile operate is the inverse distribution operate for a steady distribution. For quantile (tauin[0,1]), the conditional quantile operate implied by the (F(y|x)) in eqref{F} is
start{equation}
label{Q}tag{2}
Q(tau|x) =
(beta_0 + beta_1 x + beta_2 x^2)
left[
-ln(1-tau)
right]^{frac{1}{alpha}}
finish{equation}
For a specified worth of (x), (Q(tau|x)) produces the (tau)(th) quantile of (y) conditional on (x).
I received eqref{Q} by setting
$$
tau=1 -expleft[-left(frac{y}{
beta_0 + beta_1 x + beta_2 x^2
}right)^{alpha}right]
$$
and fixing for (y) as a operate of (tau). This inverse relationship is the muse for the interpretation of the conditional quantile curves given above. For a given (x), (F(y|x)) maps (y) into the place it ranks in ([0,1]). For a given (x), (Q(tau|x)) maps the rank (tau) into the result (y).
Estimating conditional quantile capabilities
qreg estimates the parameters of conditional quantile capabilities. Like strange least squares, the conditional quantile capabilities are assumed to be linear mixtures of covariates. Powers and interactions are accommodated utilizing issue variables.
In instance 1, I estimate (delta_0), (delta_1), and (delta_2) in (Q(0.2|x)= delta_0 + delta_1 x + delta_2 x^2).
Instance 1: qreg for 0.2 conditional quantile
. use quantile1
. qreg y x c.x#c.x, quantile(0.2)
Iteration 1: WLS sum of weighted deviations = 2549.6656
Iteration 1: sum of abs. weighted deviations = 2675.4783
Iteration 2: sum of abs. weighted deviations = 2382.9844
Iteration 3: sum of abs. weighted deviations = 2261.3777
Iteration 4: sum of abs. weighted deviations = 1855.4505
Iteration 5: sum of abs. weighted deviations = 1687.6014
Iteration 6: sum of abs. weighted deviations = 1664.1955
Iteration 7: sum of abs. weighted deviations = 1663.5237
Iteration 8: sum of abs. weighted deviations = 1661.7397
Iteration 9: sum of abs. weighted deviations = 1661.4886
Iteration 10: sum of abs. weighted deviations = 1661.485
Iteration 11: sum of abs. weighted deviations = 1661.4436
Iteration 12: sum of abs. weighted deviations = 1661.441
Iteration 13: sum of abs. weighted deviations = 1661.4379
Iteration 14: sum of abs. weighted deviations = 1661.4378
.2 Quantile regression Variety of obs = 5,000
Uncooked sum of deviations 1907.42 (about .95246261)
Min sum of deviations 1661.438 Pseudo R2 = 0.1290
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .4528183 .1370586 3.30 0.001 .1841233 .7215133
|
c.x#c.x | .3749397 .0625822 5.99 0.000 .2522511 .4976282
|
_cons | .4922369 .0650939 7.56 0.000 .3646242 .6198496
------------------------------------------------------------------------------
You’ll be able to obtain the info by clicking on this hyperlink quantile1.dta.
As mirrored within the iteration log, qreg obtains its estimates by minimizing the sum of asymmetrically weighted absolute deviations; see Koenker and Bassett (1978), Cameron and Trivedi (2010, chap. 7.2.2), and Wooldridge (2010, chap. 12.10) for particulars. The output desk presents level estimates and inference for the (delta_0), (delta_1), and (delta_2) in (Q(0.2|x)= delta_0 + delta_1 x + delta_2 x^2).
After I simulated the info, I set (beta_0=1), (beta_1=1), (beta_2=.8), and (alpha=2) in eqref{F}. These values suggest that the true values of (delta_0), (delta_1), and (delta_2) are 0.47, 0.47, and 0.38, respectively. The estimated coefficients are near their true values.
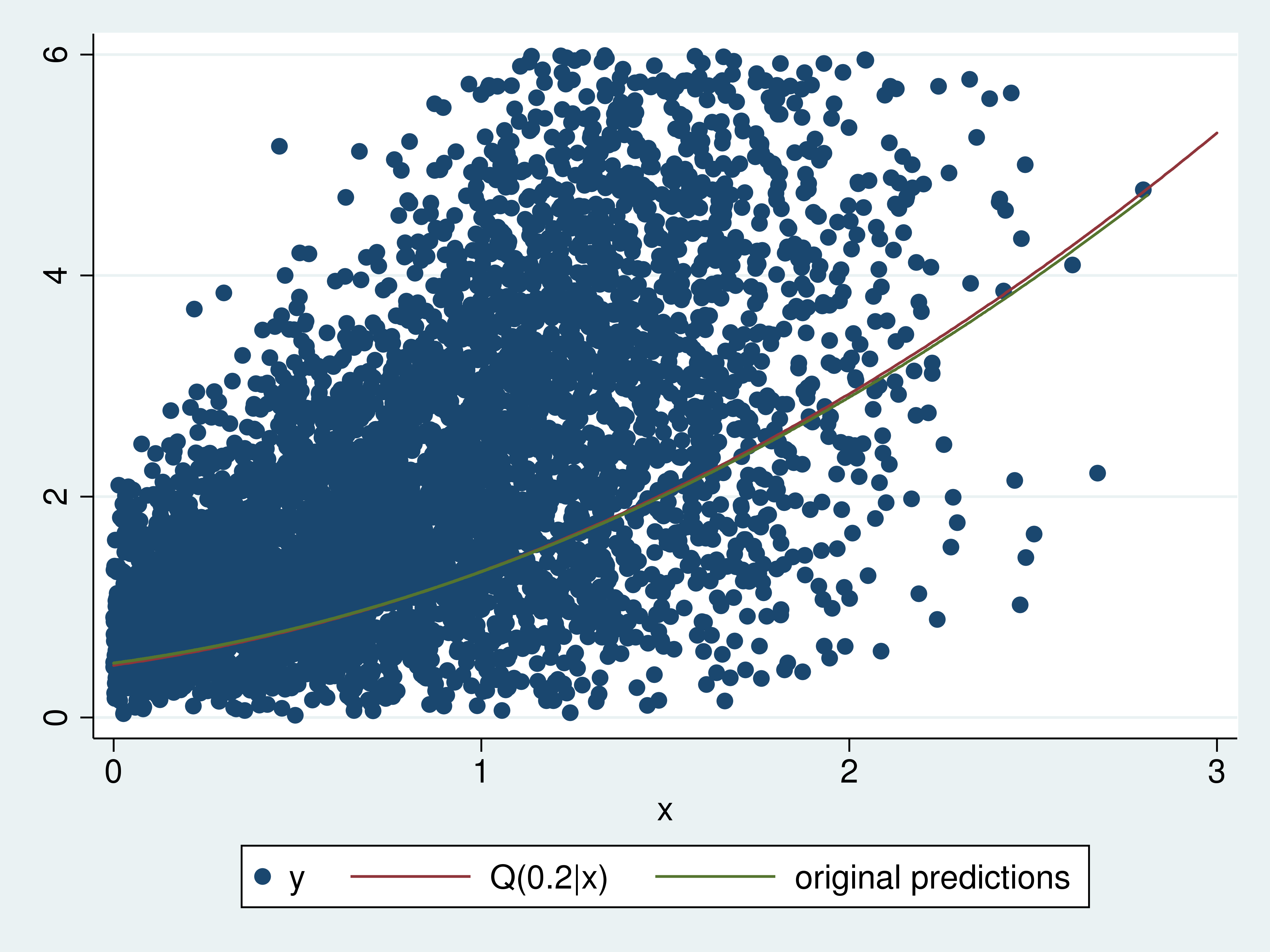
Evaluating the estimated 0.2 conditional quantiles with the true operate is one other approach of offering instinct for quantile regression. Instance 2 computes the predictions and plots them on a graph that additionally accommodates a scatterplot of a subset of the info and a plot of the true 0.2 conditional quantile operate.
Instance 2: Estimated and true 0.2 conditional quantile capabilities
. predict xb0 (choice xb assumed; fitted values) . label variable xb0 "unique predictions" . type x . twoway (scatter y x if y<6) > (operate q20 = (1+x+0.8*x^2)*((-ln(1-0.2))^(1/2)) , vary(0 3) ) > (line xb0 x) > , legend(label(2 "Q(0.2|x)")) legend(cols(3))
The estimated 0.2 conditional quantile operate could be very near the true 0.2 conditional quantile operate. Actually, I excluded bigger observations from the scatterplot in order that some distinction within the curves is obvious.
Estimating covariate results
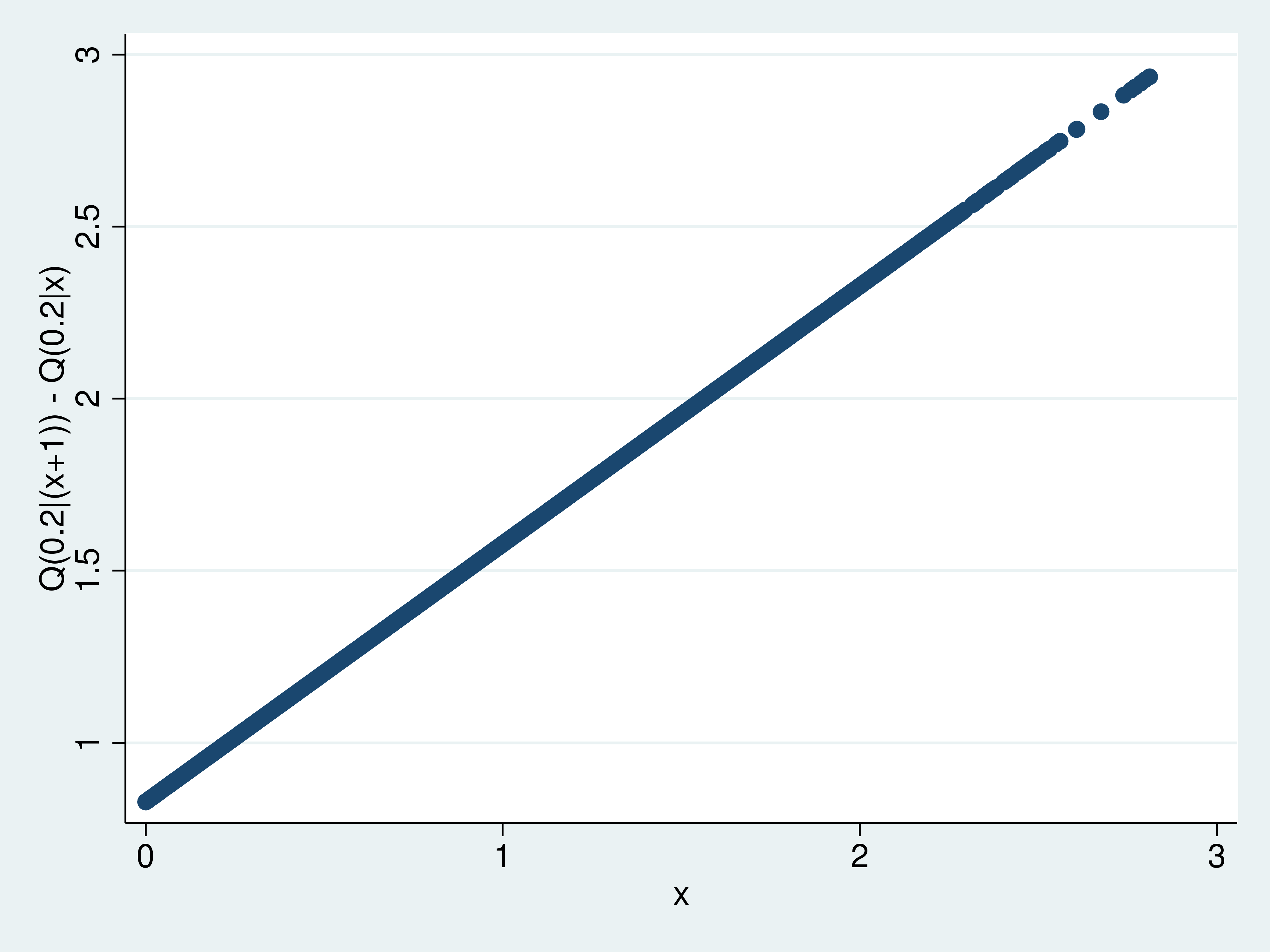
The change within the (tau)(th) conditional quantile operate that outcomes from a change in a covariate defines a covariate impact. For instance, the distinction within the 0.2 conditional quantile operate that outcomes from every unit getting an extra unit of (x) is (Q(0.2|(x+1))-Q(0.2|x)) is one such impact. Utilizing the predictions computed in instance 2, I compute and plot these estimated results in instance 3.
Instance 3: Q(0.2|(x+1))-Q(0.2|x)
. generate orig = x . substitute x = x+1 (5,000 actual modifications made) . predict xb1 (choice xb assumed; fitted values) . label variable xb1 "x=x+1 predictions" . substitute x = orig (5,000 actual modifications made) . generate results = xb1 - xb0 . label variable results "Q(0.2|(x+1)) - Q(0.2|x)" . scatter results x
This graph exhibits how the results differ over (x), however there isn’t a details about how properly these results are estimated. predictnl estimates observation-level expressions of estimated parameters and produces pointwise confidence intervals. The expression for the impact of curiosity is
_b[x] + 2*_b[c.x#c.x]*x + _b[c.x#c.x]
as a result of
_b[x]*(x+1) + _b[c.x#c.x]*(x+1)^2 + _b[_cons]
-(_b[x]*x + _b[c.x#c.x]*x^2 + _b[_cons])
= _b[x] + 2*_b[c.x#c.x]*x + _b[c.x#c.x]
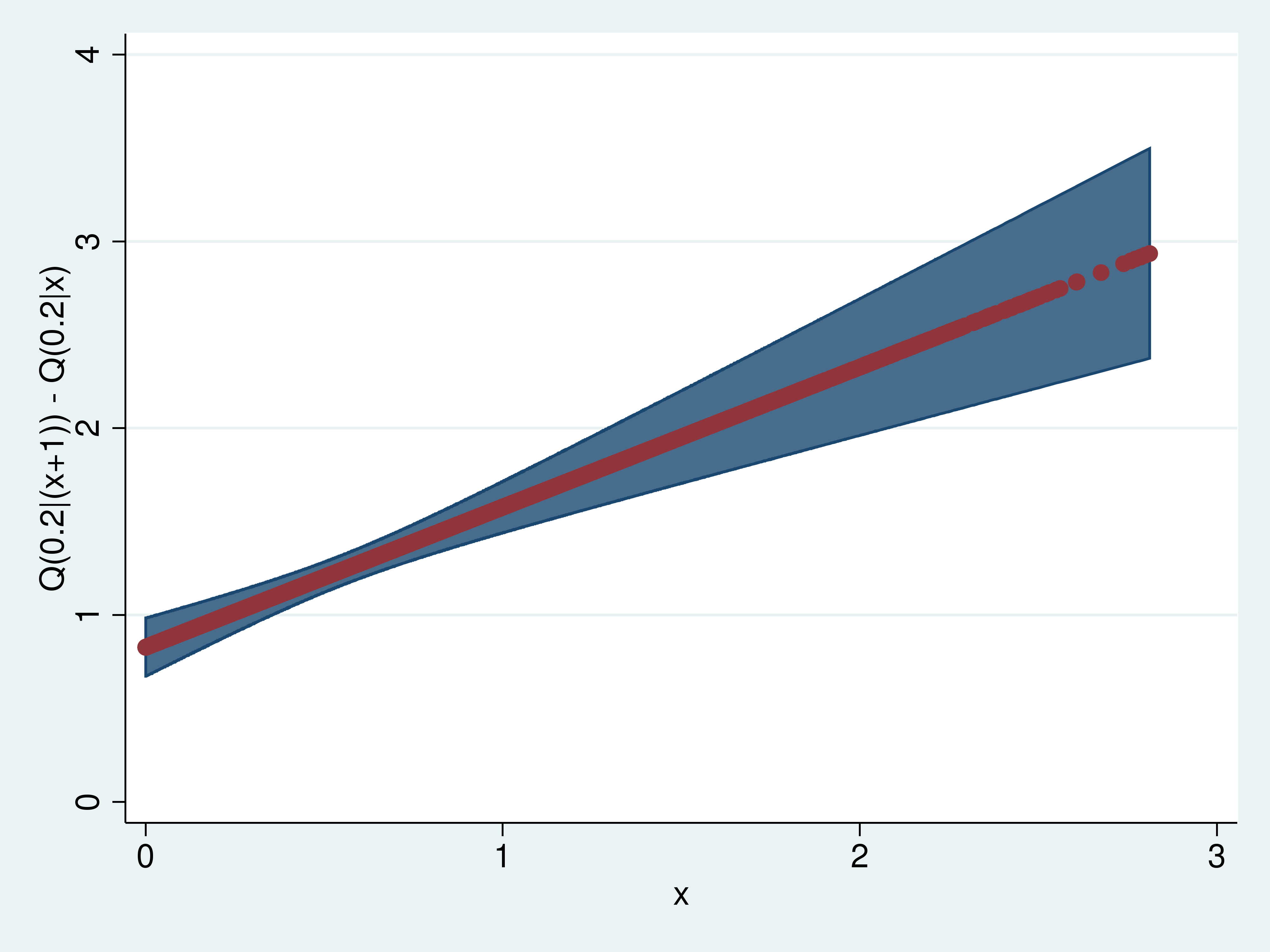
In instance 4, I exploit predictnl to compute these results and pointwise confidence intervals.
Instance 4: predictnl estimates of Q(0.2|(x+1))-Q(0.2|x)
. predictnl effects2 = _b[x] + 2*_b[c.x#c.x]*x + _b[c.x#c.x],
> ci(low up)
observe: confidence intervals calculated utilizing Z crucial values
. checklist results effects2 in 1/5
+---------------------+
| results effects2 |
|---------------------|
1. | .8279508 .8279508 |
2. | .828063 .8280631 |
3. | .8281841 .8281842 |
4. | .8283278 .8283277 |
5. | .8286009 .8286009 |
+---------------------+
. label variable effects2 "Q(0.2|(x+1)) - Q(0.2|x)"
. type x
. twoway (rarea up low x) (scatter effects2 x),
> ytitle("Q(0.2|(x+1)) - Q(0.2|x)") legend(off)
I checklist the primary 5 estimated results for instance that the 2 computations yield the identical outcomes. Having illustrated this equivalence, I plot the results with a confidence interval.
One of many causes that researchers use quantile regression is that the results can differ by quantile. The speculation is that the covariate results differ for these dealt a low rank (quantile) than for individuals who are dealt a excessive rank (quantile). To match the estimated results of an extra unit of (x) on the 0.2 conditional quantile with these results on the 0.8 conditional quantile, I start by estimating the parameters of 0.8 conditional quantile operate.
Instance 5: qreg for 0.8 conditional quantile
. qreg y x c.x#c.x, quantile(.8)
Iteration 1: WLS sum of weighted deviations = 2598.5922
Iteration 1: sum of abs. weighted deviations = 2602.1666
Iteration 2: sum of abs. weighted deviations = 2137.2076
Iteration 3: sum of abs. weighted deviations = 2060.0299
Iteration 4: sum of abs. weighted deviations = 2023.7347
Iteration 5: sum of abs. weighted deviations = 2019.0775
Iteration 6: sum of abs. weighted deviations = 1989.5983
Iteration 7: sum of abs. weighted deviations = 1984.2083
Iteration 8: sum of abs. weighted deviations = 1984.1369
Iteration 9: sum of abs. weighted deviations = 1983.9698
Iteration 10: sum of abs. weighted deviations = 1983.9663
Iteration 11: sum of abs. weighted deviations = 1983.9286
Iteration 12: sum of abs. weighted deviations = 1983.8811
Iteration 13: sum of abs. weighted deviations = 1983.8722
Iteration 14: sum of abs. weighted deviations = 1983.866
.8 Quantile regression Variety of obs = 5,000
Uncooked sum of deviations 3221.082 (about 3.7893667)
Min sum of deviations 1983.866 Pseudo R2 = 0.3841
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 1.350297 .1776428 7.60 0.000 1.002039 1.698555
|
c.x#c.x | .9258261 .0811133 11.41 0.000 .7668085 1.084844
|
_cons | 1.252304 .0843688 14.84 0.000 1.086904 1.417703
------------------------------------------------------------------------------
Whereas the output signifies that the coefficients on these phrases aren’t zero, the relative measurement of the results is just not readily obvious. In instance 6, I exploit predictnl to estimate the results of an extra unit of (x) on the 0.8 conditional quantile operate and their pointwise confidence intervals.
Instance 6: Q(0.8|(x+1))-Q(0.8|x)
. predictnl effects3 = _b[x] + 2*_b[c.x#c.x]*x + _b[c.x#c.x], > ci(low3 up3) observe: confidence intervals calculated utilizing Z crucial values . label variable effects3 "Q(0.8|(x=1)) - Q(0.8|x)"
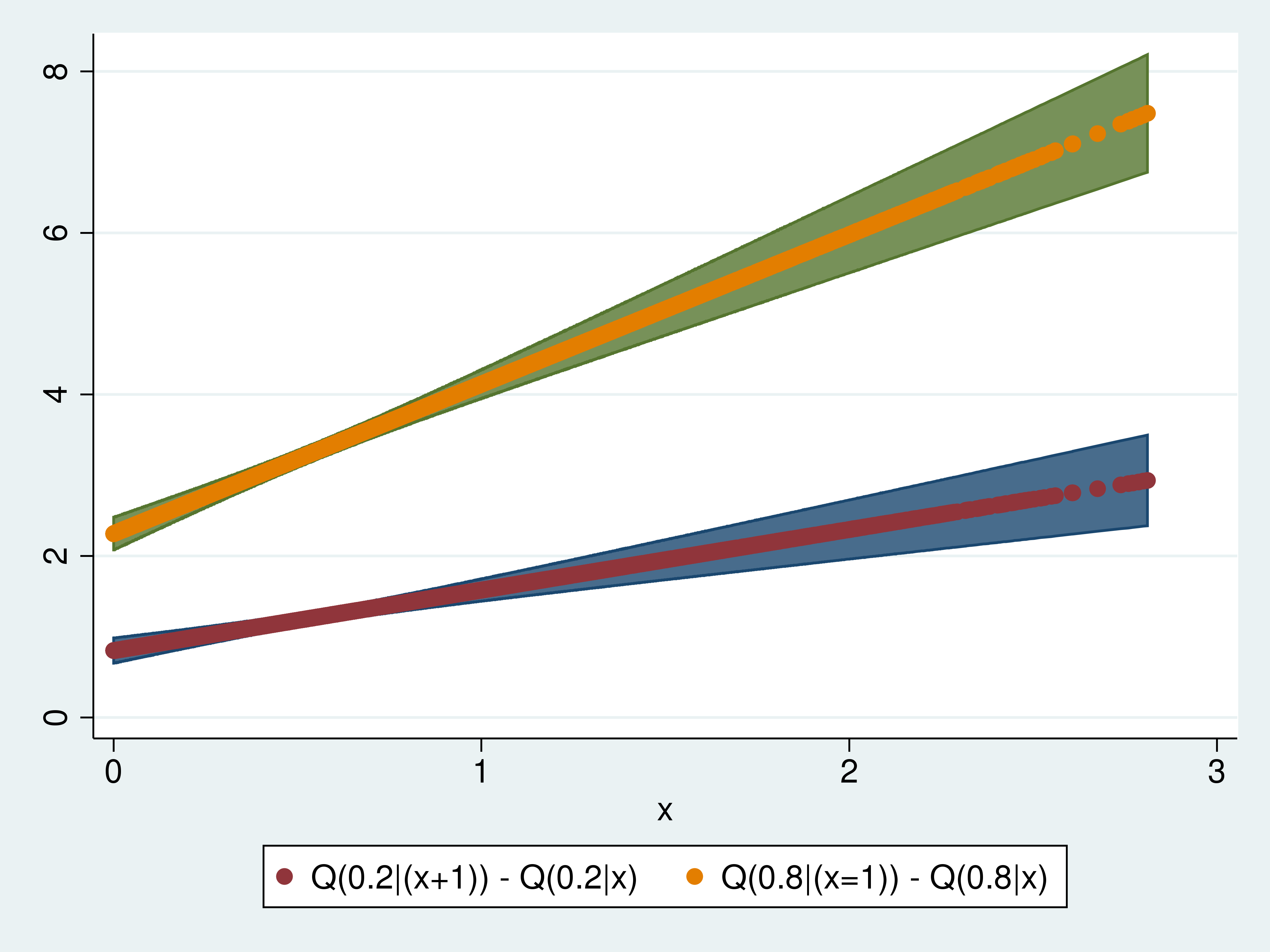
In instance 7, I plot the results of an extra unit of (x) on the 0.2 conditional quantile operate and on the 0.8 conditional quantile operate.
Each the magnitude and the slope of the results are bigger for the 0.8 conditional quantile operate than for the 0.2 conditional quantile operate.
Achieved and undone
I used simulated information for instance what conditional quantile capabilities are, and I illustrated that the results of a covariate can differ over conditional quantiles.
References
Cameron, A. C., and P. Okay. Trivedi. 2010. Microeconometrics Utilizing Stata. Rev. ed. Faculty Station, TX: Stata Press.
Koenker, R., and G. Bassett. 1978. Regression quantiles. Econometrica 46: 33–50.
Wooldridge, J. M. 2010. Econometric Evaluation of Cross Part and Panel Information. 2nd ed. Cambridge, MA: MIT Press.