Primary Idea, Instance, Demonstration in Agri Analyze and Quiz

 This weblog explains Latin Sq. Design fundamentals like when to make use of design, find out how to carry out randomization, ANOVA construction, solved instance and demonstration in Agri Analyze platform. Hyperlink of  quiz is given on the finish. (Studying time 15-20 minutes.)

Latin Sq. Design (LSD)

In agricultural discipline experiments,
fertility gradients typically run parallel to at least one aspect of the sector. Often,
these gradients run parallel to each side and in a brand new discipline, the predominant
gradient path could also be unknown. In different phrases, when the experimental discipline
is split into smaller plots (experimental items), variation can happen in a single
path, two instructions, or exhibit cyclic variation within the case of a brand new
discipline.

In animal experiments, variation
amongst experimental items will be influenced by traits reminiscent of age,
progress, physique weight, or lactation quantity. When variation is thought for a single
attribute, native management will be utilized by grouping experimental items
into blocks or replications with related traits, as seen in randomized
full block designs. This precept turns into simpler when variability
in two traits is taken into account, reminiscent of fertility gradients in two
instructions in discipline experiments or variations in age and physique weight in animal
research. Double grouping of experimental items based mostly on these traits
can considerably scale back experimental error.

The Latin sq. design exemplifies
this precept by grouping experimental items into rows and columns. For ‘t’
therapies, ‘t’ experimental items are organized into ‘t’ rows and ‘t’ columns,
making certain every remedy seems as soon as per row and column. This methodology ensures
homogeneity inside rows and columns based mostly on the 2 traits
thought of.

This design can be successfully
utilized in laboratory experiments, industrial research and soil science
analysis, the place experimental items will be grouped based mostly on two traits.

Within the Latin sq. design, double
grouping helps scale back errors attributable to variations amongst rows and columns,
providing better error discount alternatives in comparison with the randomized block
design. Every row and column comprise each remedy, permitting variations to be
attributed to soil variation. For optimum outcomes, rows and columns needs to be
related in width to equally share soil heterogeneity, leading to compact,
nearly sq. plots. Since these plots are usually small, soil variation
inside them is minimized. Not like randomized designs the place blocks needn’t be
contiguous, the latin sq. design loses its benefits if plots will not be
contiguous, making it considerably much less versatile than block designs.

In an LSD, the levels of freedom for
error are given by (t-1)(t-2), the place t is the variety of therapies. For very
small values of t the levels of freedom for error change into extraordinarily restricted,
making it troublesome to acquire dependable estimates of experimental error and
carry out legitimate statistical checks. With
greater than 10 therapies, arranging the therapies in a balanced Latin sq.
structure turns into more and more troublesome. The bodily or logistical setup of the
experiment can change into unwieldy, making it tougher to keep up the required
construction and management for row and column results. For instance for 10 therapies the variety of experimental items are 100, for 11 121 and for 12 144. The variety of experimental items will increase disproportionately making experiment incontinent for bigger therapies. 

Utility

            When
the variety of therapies ranges from 5 to 10 and experimental items will be
grouped in response to two traits in discipline experiments, animal research,
soil science analysis, industrial purposes and laboratory trials, the latin
sq. design is an acceptable and efficient selection.

Randomization and Format plan

            Randomization
within the latin sq. design entails choosing a sq. at random from all
doable Latin squares. Fisher and Yates supplied full units of latin
squares for 4 x 4 to six x 6 sizes and pattern squares as much as 12 x 12. Cochran and
Cox supplied pattern latin squares starting from 3 x 3 to 12 x 12. The
randomization methodology recommended by Cochran and Cox is as follows:

            For 3
x 3 squares: Assign letters to the therapies, which needn’t be random. Write
out a 3×3 sq., randomize the association of the three columns after which
randomize the association of the final two rows.

            For 4
x 4 squares: There are 4 distinct squares that can not be obtained from every
different by merely rearranging rows and columns. Randomly choose one in all these 4
squares after which randomly prepare all of the columns.

For five x 5 squares: Quite a few distinct
squares exist that can not be derived from each other by rearranging rows and
columns. Assign letters to the therapies randomly, then randomize all of the
columns and rows.

The required situations require
therapies to be randomized so that every remedy seems precisely as soon as in
each column and row. The best methodology to realize that is by randomly
choosing a “decreased Latin sq.” (or a Latin sq. in commonplace
kind) from the 56 commonplace Latin squares supplied within the Fisher and Yates
statistical tables for five x 5 Latin squares. A regular Latin sq. is one
the place the primary row and the primary column are organized in alphabetical order.

Procedures for randomizing therapies in LSD

Step 1: A
decreased Latin sq. or commonplace sq. was chosen randomly from the 56 Latin
squares. The random quantity chosen was 52.

Step 2: Randomization
of rows: Random numbers 3, 2, 1, 5, 4. Arranging the rows on this order.

	C1	C2	C3	C4	C5
R3	C	D	E	A	B
R2	B	C	D	E	A
R1	A	B	C	D	E
R5	E	A	B	C	D
R4	D	E	A	B	C

Step 3: Randomization of
columns: Random numbers: 3, 1, 2, 4, 5. Arranging the rows on this order we get

	C3	C1	C2	C4	C5
R3	E	C	D	A	B
R2	D	B	C	E	A
R1	C	A	B	D	E
R5	B	E	A	C	D
R4	A	D	E	B	C

Step 4: Randomization of
letters or therapies: Random numbers: 2, 5, 1, 4, 3

	C3	C1	C2	C4	C5
R3	C	A	D	B	E
R2	D	E	A	C	B
R1	A	B	E	D	C
R5	E	C	B	A	D
R4	B	D	C	E	A

The remedy random numbers are used
to switch A, B, C, D and E so as. The aim is to create a sq. such that
every remedy seems precisely as soon as in every row and column, with the therapies
allotted in a totally random order. After setting up the sq., the
experiment can be applied by making use of remedy A to the plots
akin to the positions of A’s within the remaining sq., remedy B to the
plots akin to the positions of B’s and so forth.

The experimental space
is split into plots with the variety of plots in every row and column equal to
the variety of therapies. Every remedy seems as soon as per row and column,
leading to n rows, n columns and n x n plots for n therapies. The plot form
can fluctuate from sq. to lengthy strips and the Latin sq. itself will be sq.
or rectangular. This design is very dependable for five to eight therapies, as much as a
most of 12 therapies.

Instance of LSD with Evaluation:

An
experiment on cotton was carried out to check the impact of foliar software of
urea mixed with insecticidal sprays on cotton yield. The small print of the
experiment are supplied beneath.

The therapies for the
experiment are as follows:

·      
T1
serves because the management

·      
T2
entails making use of 100 kg N/ha as urea, with 50% at remaining thinning and 50% at
flowering as high dressing

·      
T3
contains making use of 100 kg N/ha as urea, with 80 kg N/ha in 4 equal break up
doses as a twig and 20 kg/ha at remaining thinning

·      
T4
consists of making use of 100 kg N/ha as CAN (Calcium Ammonium Nitrate), with 50% at
remaining thinning and 50% at flowering as high dressing

·      
T5
combines T2 with six insecticidal sprays

·      
T6
combines T4 with six insecticidal sprays

Design structure (6 x 6)

T3 3.10	T6 5.95	T1 1.75	T5 6.40	T2 3.85	T4 5.30
T2 4.80	T1 2.70	T3 3.30	T6 5.95	T4 3.70	T5 5.40
T1 3.00	T2 2.95	T5 6.70	T4 5.95	T6 7.75	T3 7.10
T5 6.40	T4 5.80	T2 3.80	T3 6.55	T1 4.80	T6 9.40
T6 5.20	T3 4.85	T4 6.60	T2 4.60	T5 7.00	T1 5.00
T4 4.25	T5 6.65	T6 9.30	T1 4.95	T3 9.30	T2 8.40

Row/Column	C1	C2	C3	C4	C5	C6	Row complete
R1	3.10	5.95	1.75	6.40	3.85	5.30	26.35
R2	4.80	2.70	3.30	5.95	3.70	5.40	25.85
R3	3.00	2.95	6.70	5.95	7.75	7.10	33.45
R4	6.40	5.80	3.80	6.55	4.80	9.40	36.75
R5	5.20	4.85	6.60	4.60	7.00	5.00	33.25
R6	4.25	6.65	9.30	4.95	9.30	8.40	42.85
Column complete	26.75	28.9	31.45	34.4	36.4	10.6	198.50

Remedy
SS

Remedy							Remedy Complete	Remedy imply
T1	3.00	2.70	1.75	4.95	4.80	5.00	22.20	3.70
T2	4.80	2.95	3.80	4.60	3.85	8.40	28.40	4.73
T3	3.10	4.85	3.30	6.55	9.30	7.10	34.20	5.70
T4	4.25	5.80	6.60	5.95	3.70	5.30	31.60	5.27
T5	6.40	6.65	6.70	6.40	7.00	5.40	38.55	6.43
T6	5.20	5.95	9.30	5.95	7.75	9.40	43.55	7.26

Error SS

ESS = Complete SS – RSS – CSS – TSS

= 128.33 – 34.44 – 21.59 – 47.21 = 25.09

Levels
of freedom calculation

Row
= t – 1 = 6 – 1 = 5

Column
= t – 1 = 6 – 1 = 5

Error
= (t – 1) * (t-2) = 5 * 4 = 20

Complete
= complete commentary -1 = 36 – 1 = 35

Imply
Sq.

Row MS = Row SS / Row DF = 34.44 / 5  = 6.88

Column MS = Columns SS / Column DF  = 21.59 / 5 
= 4.31

Remedy MS = remedy SS / error df = 47.21 / 5 = 9.44

Error MS = error SS / error df =25.09 / 20  = 1.25

Calculated F

Row = Row MS / Error MS = 6.88 / 1.25  = 5.49

Column Cal. F = Column MS / Error MS = 4.61 / 1.25 = 3.44

Remedy Cal. F = Remedy MS / Error MS = 9.44 / 1.25 = 7.52

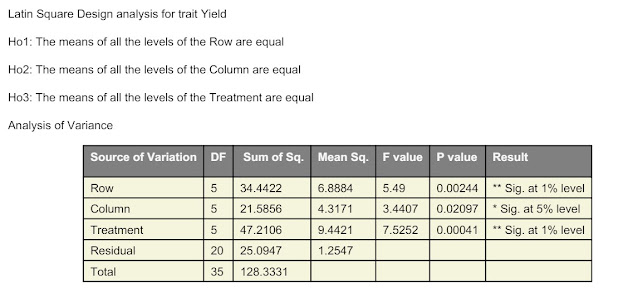
ANOVA

Supply	DF	SS	MS	Cal F
Row	5	34.44	6.88	5.49
Column	5	21.59	4.31	3.44
Remedy	5	47.21	9.44	7.52
Error	20	25.09	1.25	–
Complete	35	128.33	–	–

From the ANOVA
outcomes, the remedy impact was discovered to be vital on the 5% stage of
significance (Cal F. (7.52) > Tab F_{(0.05, 20)} (2.71)). Subsequently,
we reject the null speculation (H₀: all therapies are equal) and
conclude that at the very least one pair of therapies means are to be vital. To check
therapies means, Crucial distinction (CD) is required. 

Conclusion based mostly important distinction

Remedy T6 (100 kg N/ha as CAN + six
insecticidal sprays) resulted in a considerably increased cotton yield and was on
par with T5 (100 kg N/ha as urea + six insecticidal sprays) based mostly on important
distinction. Considerably decrease yield was noticed with T1 (management), which was
on par with T2 (100 kg N/ha utilized as urea).

Steps to carry out evaluation of LSD in Agri Analyze

Step 1: To create a CSV file
with columns for Row, Column, Remedy and Yield (Achieve)

Hyperlink of the Knowledge Set

Step 2: Go together with Agri Analyze website.  https://agrianalyze.com/Default.aspx

Step
3: Click on on ANALYTICAL TOOL

Step
4: Click on on DESIGN OF EXPERIMENT

Step
5: Click on on Latin Sq. Design Evaluation

Step
6: Choose CSV file.

Step
7: Choose remedy, row, column and dependent
variable (e.g., Yield).

Step 8: Choose a take a look at for
a number of comparisons, such because the Least Important Distinction (LSD) take a look at, to
decide vital variations amongst teams. Similar as for Duncan’s New
A number of Vary Take a look at (DNMRT), Tukey’s HSD Take a look at.

Step 9: After clicking on the submit button pay a nominal price and obtain the report.

Snips of the output file

The Weblog Submit is written by:

MSc Scholar 

Division of Agricultural Statistics

Anand Agricultural College 

Anand

You may as well try our associated blogs: