Preliminary ideas
Nonparametric regression is just like linear regression, Poisson regression, and logit or probit regression; it predicts a imply of an final result for a set of covariates. If you happen to work with the parametric fashions talked about above or different fashions that predict means, you already perceive nonparametric regression and might work with it.
The principle distinction between parametric and nonparametric fashions is the assumptions in regards to the practical type of the imply conditional on the covariates. Parametric fashions assume the imply is a identified perform of (mathbf{x}beta). Nonparametric regression makes no assumptions in regards to the practical kind.
In follow, because of this nonparametric regression yields constant estimates of the imply perform which can be sturdy to practical kind misspecification. However we don’t have to cease there. With npregress, launched in Stata 15, we might acquire estimates of how the imply modifications once we change discrete or steady covariates, and we will use margins to reply different questions in regards to the imply perform.
Under I illustrate how one can use npregress and how one can interpret its outcomes. As you will notice, the outcomes are interpreted in the identical approach you’ll interpret the outcomes of a parametric mannequin utilizing margins.
Regression instance
As an example, I’ll simulate information the place the true mannequin satisfies the linear regression assumptions. I’ll use a steady covariate and a discrete covariate. The end result modifications for various values of the discrete covariate as follows:
start{equation*}
y = left{
start{array}{cccccccl}
10 & + & x^3 & & & + &varepsilon & textual content{if} quad a=0
10 & + & x^3 & – & 10x &+ & varepsilon & textual content{if} quad a=1
10 & + & x^3 & + & 3x &+ & varepsilon & textual content{if} quad a=2
finish{array}proper.
finish{equation*}
Right here, (x) is the continual covariate and (a) is the discrete covariate with values 0, 1, and a pair of. I generate information utilizing the code under:
clear set seed 111 set obs 1000 generate x = rnormal(1,1) generate a = int(runiform()*3) generate e = rnormal() generate gx = 10 + x^3 if a==0 substitute gx = 10 + x^3 - 10*x if a==1 substitute gx = 10 + x^3 + 3*x if a==2 generate y = gx + e
Typically the imply perform is just not identified to the researchers. If I knew the true practical relationship between (y), (a), and (x), I may use regress to estimate the imply perform. For now, I assume I do know the true relationship and estimate the imply perform by typing
. regress y c.x#c.x#c.x c.x#i.a
Then I calculate the typical of the imply perform, the typical marginal impact of (x), and common remedy results of (a).
The typical of the imply perform is estimated to be (12.02), which I obtained by typing
. margins
Predictive margins Variety of obs = 1,000
Mannequin VCE : OLS
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | 12.02269 .0313691 383.26 0.000 11.96114 12.08425
------------------------------------------------------------------------------
The typical marginal impact of of (x) is estimated to be (3.96), which I obtained by typing
. margins, dydx(x)
Common marginal results Variety of obs = 1,000
Mannequin VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : x
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 3.957383 .0313871 126.08 0.000 3.89579 4.018975
------------------------------------------------------------------------------
The typical remedy impact of (a=1), relative to (a=0), is estimated to be (-9.78). The typical remedy impact of (a=2), relative to (a=0), is estimated to be (3.02). I obtained these by typing
. margins, dydx(a)
Common marginal results Variety of obs = 1,000
Mannequin VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : 1.a 2.a
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
a |
1 | -9.776916 .0560362 -174.47 0.000 -9.886879 -9.666953
2 | 3.019998 .0519195 58.17 0.000 2.918114 3.121883
------------------------------------------------------------------------------
Notice: dy/dx for issue ranges is the discrete change from the bottom degree.
I now use npregress to estimate the imply perform, making no assumptions in regards to the practical kind:
. npregress kernel y x i.a, vce(bootstrap, reps(100) seed(111))
(working npregress on estimation pattern)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Bandwidth
------------------------------------
| Imply Impact
-------------+----------------------
Imply |
x | .3630656 .5455175
a | 3.05e-06 3.05e-06
------------------------------------
Native-linear regression Variety of obs = 1,000
Steady kernel : epanechnikov E(Kernel obs) = 363
Discrete kernel : liracine R-squared = 0.9888
Bandwidth : cross validation
------------------------------------------------------------------------------
| Noticed Bootstrap Percentile
y | Estimate Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Imply |
y | 12.34335 .3195918 38.62 0.000 11.57571 12.98202
-------------+----------------------------------------------------------------
Impact |
x | 3.619627 .2937529 12.32 0.000 3.063269 4.143166
|
a |
(1 vs 0) | -9.881542 .3491042 -28.31 0.000 -10.5277 -9.110781
(2 vs 0) | 3.168084 .2129506 14.88 0.000 2.73885 3.570004
------------------------------------------------------------------------------
Notice: Impact estimates are averages of derivatives for steady covariates
and averages of contrasts for issue covariates.
The typical of the imply estimate is (12.34), the typical marginal impact of (x) is estimated to be (3.62), the typical remedy impact of (a=1) is estimated to be (-9.88), and the typical remedy impact of (a=2) is estimated to be (3.17). All values are fairly near those I obtained utilizing regress after I assumed I knew the true imply perform.
Moreover, the boldness interval for every estimate contains each the true parameter worth I simulated and the regress parameter estimate. This highlights one other essential level. Generally, the boldness intervals I acquire from npregress are wider than these from regress with the appropriately specified mannequin. This isn’t shocking. Nonparametric regression is constant, nevertheless it can’t be extra environment friendly than becoming a appropriately specified parametric mannequin.
Utilizing regress and margins and realizing the practical type of the imply is equal to utilizing npregress on this instance. You get related level estimates and the outcomes have the identical interpretation.
Binary final result instance
Above I introduced a end result for a steady final result. Nevertheless, the result doesn’t must be steady. I can estimate a conditional imply, which is identical because the conditional likelihood, for binary outcomes.
The true mannequin is given by
start{equation*}
y = left{
start{array}{cl}
1 & textual content{if} quad -1 + x – a + varepsilon > 0
0 & textual content{in any other case}
finish{array}proper.
finish{equation*}
the place
start{equation*}
varepsilon | x, a sim mathrm{Logistic} left(0, frac{pi}{sqrt{3}} proper)
finish{equation*}
And (a) once more takes on discrete values 0, 1, and a pair of. The outcomes of estimation utilizing logit could be
. quietly logit y x i.a
. margins
Predictive margins Variety of obs = 1,000
Mannequin VCE : OIM
Expression : Pr(y), predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | .486 .0137 35.47 0.000 .4591485 .5128515
------------------------------------------------------------------------------
. margins, dydx(*)
Common marginal results Variety of obs = 1,000
Mannequin VCE : OIM
Expression : Pr(y), predict()
dy/dx w.r.t. : x 1.a 2.a
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .1984399 .0117816 16.84 0.000 .1753483 .2215315
|
a |
1 | -.1581501 .0347885 -4.55 0.000 -.2263344 -.0899658
2 | -.363564 .0319078 -11.39 0.000 -.426102 -.3010259
------------------------------------------------------------------------------
Notice: dy/dx for issue ranges is the discrete change from the bottom degree.
The typical of the conditional imply estimate is (0.486), which is identical as the typical likelihood of a optimistic final result; the marginal impact of (x) is estimated to be (0.198), the typical remedy results of (a=1) is estimated to be (-0.158), and the typical remedy results of (a=2) is estimated to be (-0.364).
Let’s see if npregress can acquire related outcomes with out realizing the practical kind is logistic.
. npregress kernel y x i.a, vce(bootstrap, reps(100) seed(111))
(working npregress on estimation pattern)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Bandwidth
------------------------------------
| Imply Impact
-------------+----------------------
Imply |
x | .4321719 1.410937
a | .4 .4
------------------------------------
Native-linear regression Variety of obs = 1,000
Steady kernel : epanechnikov E(Kernel obs) = 432
Discrete kernel : liracine R-squared = 0.2545
Bandwidth : cross validation
------------------------------------------------------------------------------
| Noticed Bootstrap Percentile
y | Estimate Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Imply |
y | .4840266 .0160701 30.12 0.000 .4507854 .5158817
-------------+----------------------------------------------------------------
Impact |
x | .2032644 .0143028 14.21 0.000 .1795428 .2350924
|
a |
(1 vs 0) | -.1745079 .0214352 -8.14 0.000 -.2120486 -.1249168
(2 vs 0) | -.3660315 .0331167 -11.05 0.000 -.4321482 -.300859
------------------------------------------------------------------------------
Notice: Impact estimates are averages of derivatives for steady covariates and
averages of contrasts for issue covariates.
The conditional imply estimate is (0.484), the marginal impact of (x) is estimated to be (0.203), the typical remedy results of (a=1) is estimated to be (-0.174), and the typical remedy results of (a=2) is estimated to be (-0.366). So, sure, it might probably.
Answering different questions
npregress gives marginal results and common remedy impact estimates as a part of its final result, but I also can acquire solutions to different related questions utilizing margins.
Let’s return to the regression instance.
Say I wished to see the imply perform at totally different values of the covariate (x), averaging over (a). I may kind:
. margins, at(x=(1(.5)3)) vce(bootstrap, reps(100) seed(111))
(working margins on estimation pattern)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Predictive margins Variety of obs = 1,000
Replications = 100
Expression : imply perform, predict()
1._at : x = 1
2._at : x = 1.5
3._at : x = 2
4._at : x = 2.5
5._at : x = 3
------------------------------------------------------------------------------
| Noticed Bootstrap Percentile
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | 9.309943 .1538459 60.51 0.000 9.044058 9.689572
2 | 10.96758 .2336364 46.94 0.000 10.53089 11.52332
3 | 14.78267 .311172 47.51 0.000 14.21305 15.50895
4 | 21.50949 .3955136 54.38 0.000 20.86696 22.34698
5 | 32.16382 .529935 60.69 0.000 31.10559 33.25611
------------------------------------------------------------------------------
after which, utilizing marginsplot, I acquire the next graph:
Determine 1: Imply final result at totally different values of x
As (x) will increase, so does the result. The rise is nonlinear. It’s a lot larger for bigger values of (x) than for smaller ones.
I may as an alternative hint the imply perform for various values of (x), however now, acquiring the anticipated imply for every degree of (a) relatively than averaging over (a), I kind
. margins a, at(x=(-1(1)3)) vce(bootstrap, reps(100) seed(111))
after which use marginsplot to visualise the outcomes:
Determine 2: Imply final result at totally different values of x for mounted values of a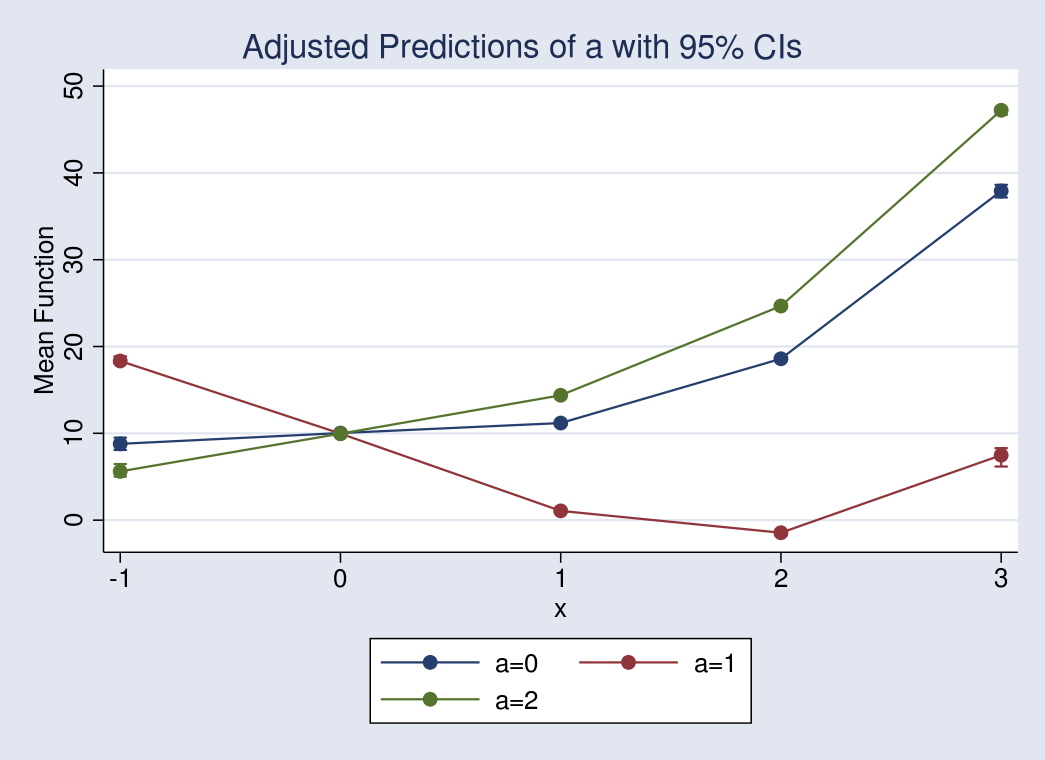
I see that the impact on the imply, as (x) will increase, differs for various values of (a). As a result of our mannequin has solely two covariates, the graph above maps the entire imply perform.
I may even ask what the typical impact of a ten% enhance in (x) is. By “common” on this case, I imply giving every remark within the dataset a ten% bigger (x). Maybe (x) is a rebate and I ponder what would occur if that rebate have been elevated by 10%. I kind
. margins, at(x=generate(x*1.1)) at(x=generate(x))
> distinction(at(r) nowald) vce(bootstrap, reps(100) seed(111))
(working margins on estimation pattern)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Contrasts of predictive margins
Variety of obs = 1,000
Replications = 100
Expression : imply perform, predict()
1._at : x = x*1.1
2._at : x = x
--------------------------------------------------------------
| Noticed Bootstrap Percentile
| Distinction Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
_at |
(2 vs 1) | -1.088438 .0944531 -1.31468 -.915592
--------------------------------------------------------------
I can use margins and npregress collectively to acquire results at totally different factors in my information, common results over my inhabitants, or any query that might make sense with a parametric mannequin in Stata.
Closing remarks
npregress estimates a imply perform with all forms of outcomes—steady, binary, depend outcomes, and extra. The interpretation of the outcomes is equal to the interpretation, and their usefulness is equal to that of margins after becoming a parametric mannequin. What makes npregress particular is that we don’t have to assume a practical kind. With parametric fashions, our inferences will possible be meaningless if we have no idea the true practical kind. With npregress, our inferences are legitimate whatever the true practical kind.

