AlmostSure on X identified that
log2 3 ≈ 19/12,
an approximation that’s fairly good relative to the dimensions of the denominator. To get an approximation that’s as correct or higher requires a bigger denominator for log2 5.
log2 5 ≈ 65/28
This above observations are right, however are they indicative of a extra common sample? Is log2 3 simpler to approximate than log2 5 utilizing rational numbers? There are theoretical methods to quantify this—irrationality measures—however they’re arduous to compute.
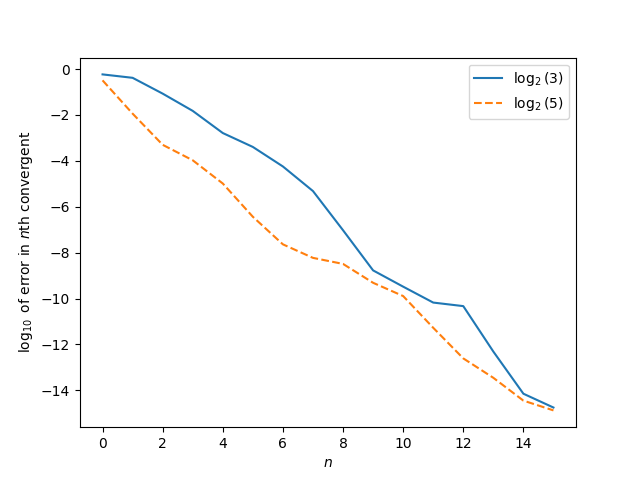
For those who have a look at the sequence of approximations for each numbers, primarily based on continued fraction convergents, the nth convergent for log2 5 is extra correct than the nth convergent for log2 3, at the very least for the primary 16 phrases. After that I ran out of floating level precision and wasn’t sufficiently to resort to prolonged precision.
Admittedly this can be a non-standard approach to consider approximation error. Usually you have a look at the approximation error relative to the dimensions of the denominator, not relative to the index of the convergents.
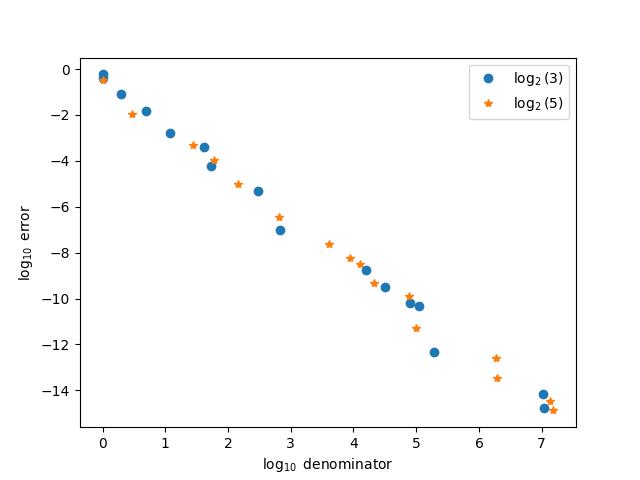
Right here’s a extra typical comparability, plotting the log of approximation error towards the log of the denominators.
Continued fraction posts
- Continued fractions as matrix merchandise
- Purposes of continued fractions
- Calendars and continued fractions
The publish log2(3) and log2(5) first appeared on John D. Cook dinner.