The inverse of the matrix
is the matrix
assuming advert − bc ≠ 0.
Additionally, the inverse of the bilinear operate (a.okay.a. Möbius transformation)
is the operate
once more assuming advert − bc ≠ 0.
The elementary takeaway is that listed here are two helpful equations which can be related in look, so memorizing one makes it straightforward to memorize the opposite. We might cease there, however let’s dig slightly deeper.
There’s apparently an affiliation between 2 × 2 matrices and Möbius transformations
This affiliation is so robust that we will use it to compute the inverse of a Möbius transformation by going to the related matrix, inverting it, and going again to a Möbius transformation. In diagram type, we now have the next
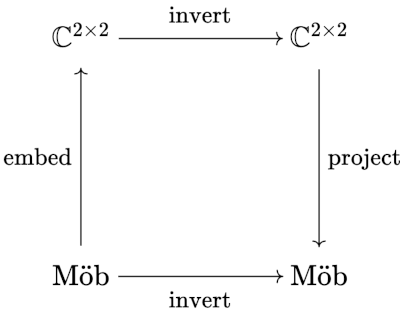
Now there are just a few lose ends. Initially, we don’t actually have a map between Möbius transformations and matrices per se; we now have a map between a explicit illustration of a Möbius transformation and a 2 × 2 matrix. If we multiplied a, b, c, and d in a Möbius transformation by 10, for instance, we’d nonetheless have the identical transformation, only a totally different illustration, however it will go to a unique matrix.
What we actually have a map between Möbius transformations and equivalence lessons of invertible matrices, the place two matrices are equal if one is a non-zero a number of of the opposite. If we wished to make the diagram above extra rigorous, we’d substitute ℂ2×2 with PL(2, ℂ), linear transformations on the advanced projective airplane. In refined phrases, our map between Möbius transformations and matrices is an isomorphism between automorphisms of the Riemann sphere and PL(2, ℂ).
Möbius transformations act loads like linear transformations as a result of they are linear transformations, however on the advanced projective airplane, not on the advanced numbers. Extra on that right here.
