Desk of Contents
Introduction to KV Cache Optimization Utilizing Grouped Question Consideration
Giant language fashions excel at processing in depth contexts, enabling them to generate coherent essays, perform multi-step reasoning, and preserve conversational threads over 1000’s of tokens. Nonetheless, as sequence lengths develop, so do the computational and reminiscence calls for throughout autoregressive decoding. Engineers should steadiness maximizing context window dimension and staying inside {hardware} limits.
On the coronary heart of this problem lies the key-value (KV) cache, which shops each previous key and worth tensor for every consideration head, thereby avoiding redundant computations. Whereas caching accelerates per-token technology, its reminiscence footprint scales linearly with the variety of consideration heads, sequence size, and mannequin depth. Left unchecked, KV cache necessities can balloon to tens of gigabytes, forcing trade-offs in batch dimension or context size.
Grouped Question Consideration (GQA) provides a center floor by reassigning a number of question heads to share a smaller set of KV heads. This easy but highly effective adjustment reduces KV cache dimension and not using a substantial impression on mannequin accuracy.
On this submit, we’ll discover the basics of KV cache, examine consideration variants, derive memory-savings math, stroll via code implementations, and share best-practice suggestions for tuning and deploying GQA-optimized fashions.
This lesson is the first of a 3-part sequence on LLM Inference Optimization — KV Cache:
- Introduction to KV Cache Optimization Utilizing Grouped Question Consideration (this tutorial)
- KV Cache Optimization through Multi-Head Latent Consideration
- KV Cache Optimization through Tensor Product Consideration
To discover ways to optimize KV Cache utilizing Grouped Question Consideration, simply hold studying.
Understanding the KV Cache
Transformers compute, for every token in a sequence, three projections: queries 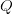 , keys
, keys 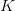 , and values
, and values 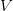 . Throughout autoregressive technology, at step
. Throughout autoregressive technology, at step 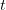 , the mannequin should attend to all earlier tokens
, the mannequin should attend to all earlier tokens 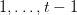 .
.
With out caching, one would recompute
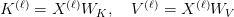
for each layer 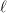 and each previous token — an
and each previous token — an 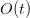 value per token that rapidly turns into prohibitive.
value per token that rapidly turns into prohibitive.
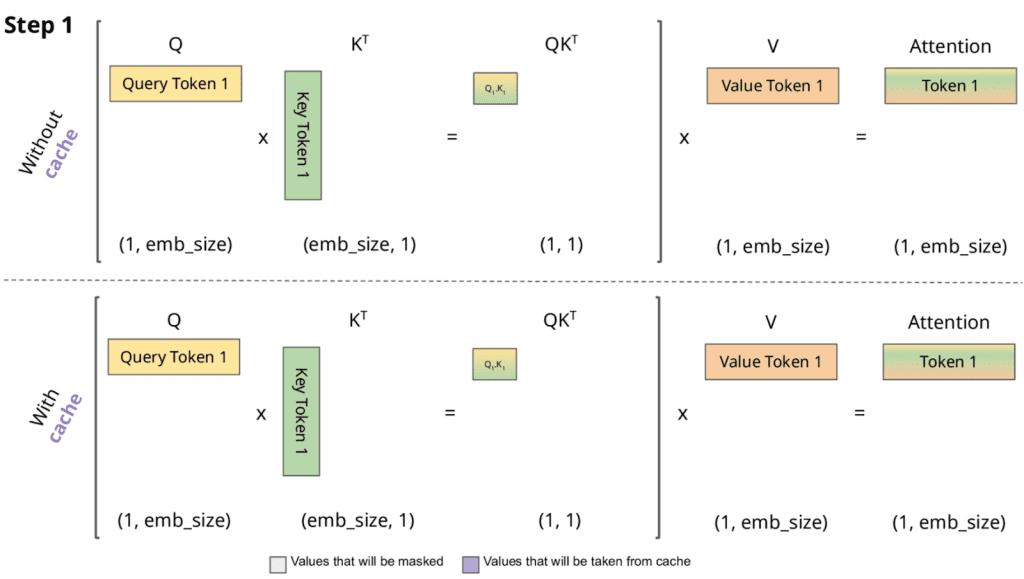
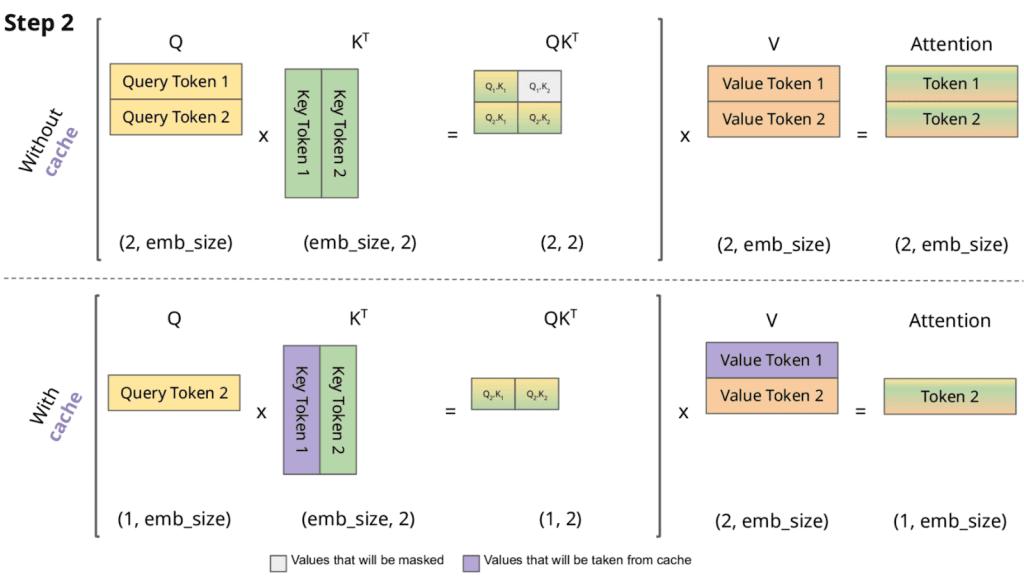
KV caching sidesteps this by storing the previous keys and values in reminiscence as they’re first computed, in order that at step 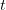 , the mannequin solely must compute
, the mannequin solely must compute
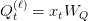
after which carry out consideration towards the cached 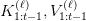 (Figures 1 and a pair of).
(Figures 1 and a pair of).
As a result of every consideration head 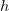 at layer
at layer 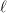 maintains its personal key and worth sequences of dimension
maintains its personal key and worth sequences of dimension 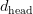 , the cache for that head and layer grows linearly within the context size
, the cache for that head and layer grows linearly within the context size 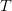 .
.
Concretely, if there are 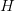 consideration heads, and we retailer each keys and values in 2 bytes (FP16) per component, the per-layer KV cache dimension is
consideration heads, and we retailer each keys and values in 2 bytes (FP16) per component, the per-layer KV cache dimension is
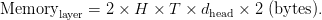
Over  layers and a batch of dimension
layers and a batch of dimension 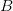 , the entire KV cache requirement turns into
, the entire KV cache requirement turns into
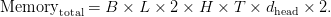
Past uncooked storage, every new token’s consideration computation should scan via the complete cached sequence, yielding a compute value proportional to
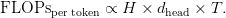
Thus, each reminiscence bandwidth (studying 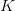 ,
, 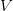 ) and computation (dot-product of
) and computation (dot-product of 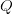 towards all cached keys) scale linearly with the rising context.
towards all cached keys) scale linearly with the rising context.
KV caching dramatically reduces the work of recomputing (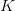 ) and (
) and (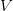 ), but it surely additionally makes the cache’s dimension and structure a first-class concern when pushing context home windows into the 1000’s of tokens.
), but it surely additionally makes the cache’s dimension and structure a first-class concern when pushing context home windows into the 1000’s of tokens.
Grouped Question Consideration
What Is Grouped Question Consideration?
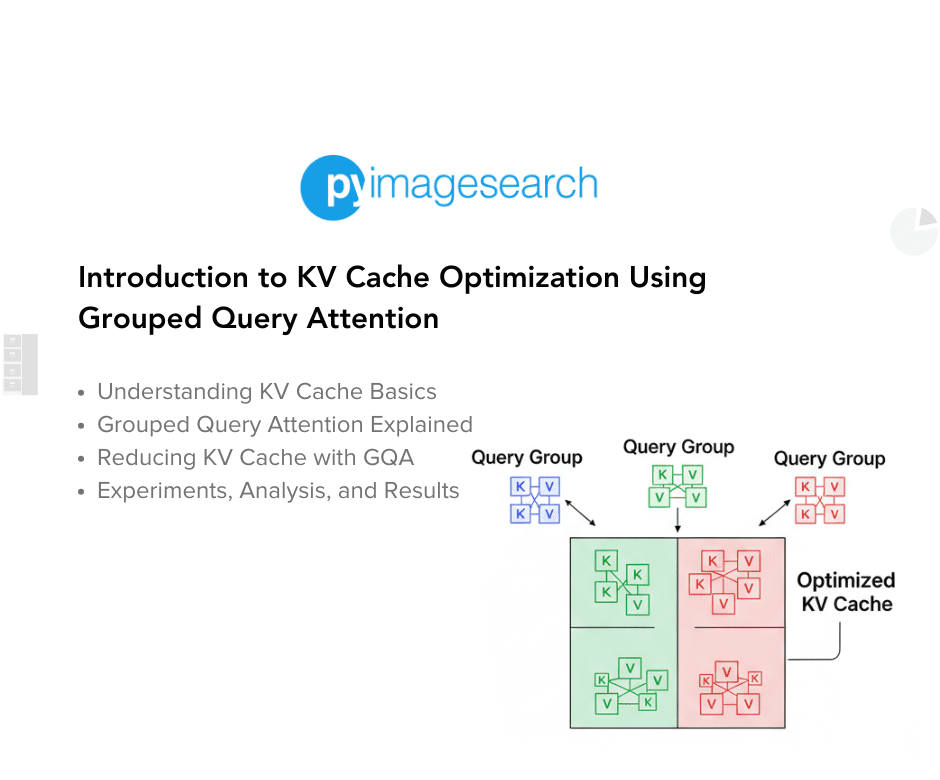
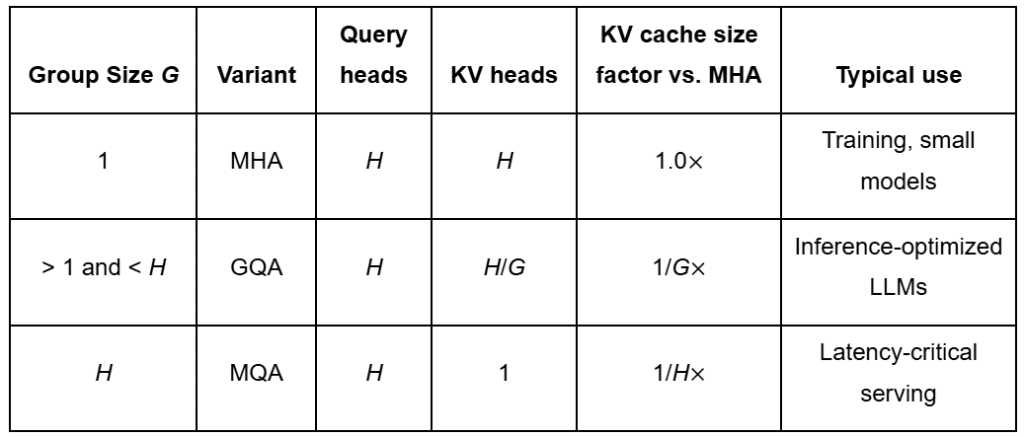
Grouped Question Consideration (GQA) modifies the usual multi-head consideration (MHA) by having a number of question heads share a lowered set of key and worth heads (Determine 3).
In vanilla MHA, the variety of key heads 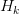 and worth heads
and worth heads 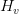 equals the variety of question heads
equals the variety of question heads 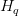 :
:
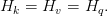
GQA introduces a grouping issue 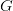 in order that
in order that
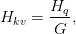
which means every group of 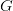 question heads attends to a single shared key and worth head.
question heads attends to a single shared key and worth head.
Regardless of this sharing, the question projections stay one per head:
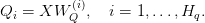
Keys and values are computed solely per group: for group index 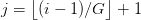 , we now have
, we now have
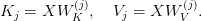
Throughout consideration, every question head 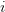 makes use of the shared pair
makes use of the shared pair 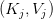 :
:
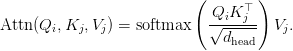
By chopping the variety of key and worth projections from 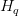 to
to 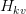 , GQA reduces each the parameter depend in
, GQA reduces each the parameter depend in 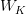 and
and 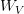 and the reminiscence wanted to retailer their outputs, whereas leaving the general mannequin dimension and ultimate output projection unchanged.
and the reminiscence wanted to retailer their outputs, whereas leaving the general mannequin dimension and ultimate output projection unchanged.
Primarily based on totally different values of 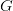 , we are able to categorize consideration into the next sorts (Desk 1):
, we are able to categorize consideration into the next sorts (Desk 1):
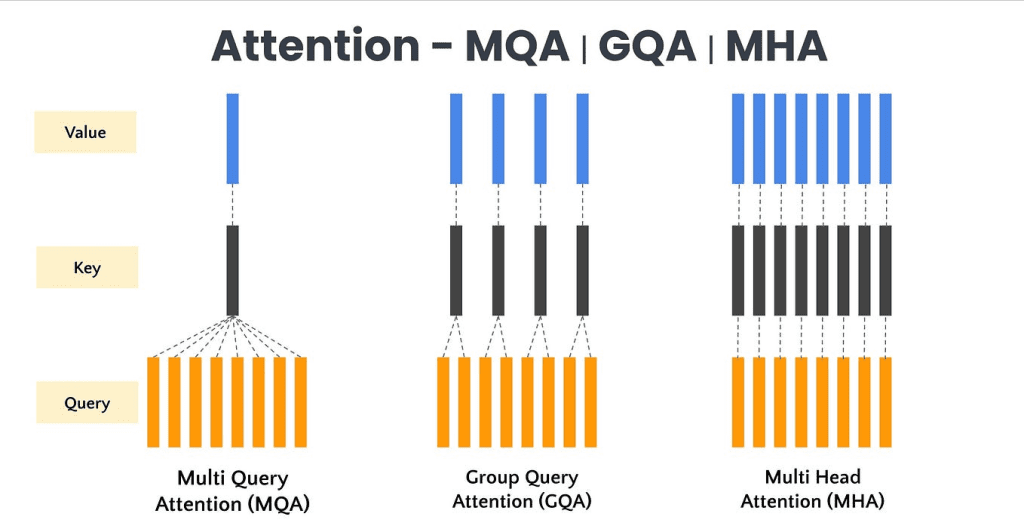
How Grouped Question Consideration Reduces KV Cache?
The KV cache shops previous key and worth tensors of form ![[Ttimes d_{text{head}}] [Ttimes d_{text{head}}]](https://b2633864.smushcdn.com/2633864/wp-content/latex/341/34197615c404759fe8a2a01c44b308ce-ffffff-000000-0.png?lossy=2&strip=1&webp=1) for every head, the place
for every head, the place 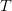 is the present context size, and
is the present context size, and 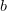 is the bytes per component (e.g., 2 for FP16).
is the bytes per component (e.g., 2 for FP16).
In customary MHA, the per-layer cache reminiscence is
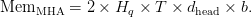
Below GQA, solely 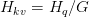 key and worth heads are saved, giving
key and worth heads are saved, giving

Thus, the cache dimension shrinks by an element of (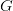 ):
):
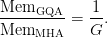
Importantly, the compute value of the dot-product consideration — proportional to 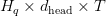 — stays the identical.
— stays the identical.
This decouples reminiscence bandwidth from FLOPs, so decreasing the cache immediately interprets to quicker long-context inference with out altering per-token computational load.
Implementing KV Caching through Grouped Question Consideration
On this part, we’ll see how utilizing Grouped Question Consideration improves the inference time and KV Cache dimension. For simplicity, we’ll implement a toy transformer mannequin with 1 layer of a Grouped Question Consideration layer.
Grouped Question Consideration
We are going to begin by implementing the Grouped Question Consideration in PyTorch.
import torch
import torch.nn as nn
import time
import matplotlib.pyplot as plt
class GroupedQueryAttention(nn.Module):
def __init__(self, hidden_dim, num_heads, group_size=1):
tremendous().__init__()
self.hidden_dim = hidden_dim
self.num_heads = num_heads
self.group_size = group_size
self.kv_heads = num_heads // group_size
self.head_dim = hidden_dim // num_heads
self.q_proj = nn.Linear(hidden_dim, hidden_dim)
self.k_proj = nn.Linear(hidden_dim, self.kv_heads * self.head_dim)
self.v_proj = nn.Linear(hidden_dim, self.kv_heads * self.head_dim)
self.out_proj = nn.Linear(hidden_dim, hidden_dim)
def ahead(self, x, kv_cache):
batch_size, seq_len, _ = x.dimension()
# Venture queries, keys, values
q = self.q_proj(x).view(batch_size, seq_len, self.num_heads, self.head_dim).transpose(1, 2)
okay = self.k_proj(x).view(batch_size, seq_len, self.kv_heads, self.head_dim).transpose(1, 2)
v = self.v_proj(x).view(batch_size, seq_len, self.kv_heads, self.head_dim).transpose(1, 2)
# Append to cache
kv_cache['k'] = torch.cat([kv_cache['k'], okay], dim=2)
kv_cache['v'] = torch.cat([kv_cache['v'], v], dim=2)
# Increase KV heads to match question heads
k_exp = kv_cache['k'].repeat_interleave(self.group_size, dim=1)
v_exp = kv_cache['v'].repeat_interleave(self.group_size, dim=1)
# Scaled dot-product consideration
scores = torch.matmul(q, k_exp.transpose(-2, -1)) / (self.head_dim ** 0.5)
weights = torch.nn.practical.softmax(scores, dim=-1)
attn_output = torch.matmul(weights, v_exp)
# Merge heads
attn_output = attn_output.transpose(1, 2).contiguous().view(batch_size, seq_len, self.hidden_dim)
return self.out_proj(attn_output), kv_cache
We outline a grouped question consideration module on Traces 6-13. Right here, we inherit from nn.Module and seize the primary dimensions: hidden_dim, num_heads, and group_size. We compute kv_heads = num_heads // group_size to find out what number of key and worth heads we’ll truly challenge, and head_dim = hidden_dim // num_heads because the dimension per question head.
On Traces 15-18, we instantiate 4 linear layers: one every for projecting queries (q_proj), keys (k_proj), and values (v_proj), and a ultimate out_proj to recombine the attended outputs again into the mannequin’s hidden house.
On Traces 20-27, the ahead methodology begins by unpacking batch_size and seq_len from the enter tensor x. We then challenge x into queries, keys, and values. Queries are formed into (batch, num_heads, seq_len, head_dim) on Line 24, whereas keys and values use (batch, kv_heads, seq_len, head_dim) on Traces 25 and 26.
On Traces 29 and 30, we append these newly computed key and worth tensors alongside the time dimension into kv_cache, preserving all previous context for autoregressive decoding.
Subsequent, we align the cached key and worth heads to match the variety of question heads. On Traces 33 and 34, we use repeat_interleave to broaden every group’s cached (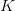 ,
, 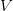 ) from
) from kv_heads to num_heads so each question head can attend.
On Traces 37-39, we implement scaled dot-product consideration: we compute uncooked scores through q @ k_expᵀ divided by √head_dim, apply softmax to acquire consideration weights, after which multiply by v_exp to provide the attended outputs.
Lastly, on Traces 41-43, we merge the per‐head outputs again to (batch, seq_len, hidden_dim) and go them via out_proj, returning each the up to date consideration output and the expanded kv_cache.
Toy Transformer and Inference
Now that we now have carried out the grouped question consideration module, we’ll implement a 1-layer toy Transformer block that takes a sequence of enter tokens, together with KV Cache, and performs one feedforward go.
class TransformerBlock(nn.Module):
def __init__(self, hidden_dim, num_heads, group_size=1):
tremendous().__init__()
self.attn = GroupedQueryAttention(hidden_dim, num_heads, group_size)
self.norm1 = nn.LayerNorm(hidden_dim)
self.ff = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim * 4),
nn.ReLU(),
nn.Linear(hidden_dim * 4, hidden_dim)
)
self.norm2 = nn.LayerNorm(hidden_dim)
def ahead(self, x, kv_cache):
attn_out, kv_cache = self.attn(x, kv_cache)
x = self.norm1(x + attn_out)
ff_out = self.ff(x)
x = self.norm2(x + ff_out)
return x, kv_cache
We outline a TransformerBlock class on Traces 1-11, the place the constructor wires collectively a grouped MultiHeadAttention layer (self.attn), two LayerNorms (self.norm1 and self.norm2), and a two-layer feed-forward community (self.ff) that expands the hidden dimension by 4× after which tasks it again.
On Traces 13-18, the ahead methodology takes enter x and the kv_cache, runs x via the eye module to get attn_out and an up to date cache, then applies a residual connection plus layer norm (x = norm1(x + attn_out)).
Subsequent, we feed this via the FFN, add one other residual connection, normalize once more (x = norm2(x + ff_out)), and at last return the reworked hidden states alongside the refreshed kv_cache.
The code under runs an inference to generate a sequence of tokens in an autoregressive method.
def run_inference(block, group_size=1):
hidden_dim = block.attn.hidden_dim
num_heads = block.attn.num_heads
seq_lengths = checklist(vary(1, 101, 10))
kv_cache_sizes = []
inference_times = []
kv_cache = {
'okay': torch.empty(1, num_heads // group_size, 0, hidden_dim // num_heads),
'v': torch.empty(1, num_heads // group_size, 0, hidden_dim // num_heads)
}
for seq_len in seq_lengths:
x = torch.randn(1, 1, hidden_dim) # One token at a time
begin = time.time()
_, kv_cache = block(x, kv_cache)
finish = time.time()
dimension = kv_cache['k'].numel() + kv_cache['v'].numel()
kv_cache_sizes.append(dimension)
inference_times.append(finish - begin)
return seq_lengths, kv_cache_sizes, inference_times
On Traces 1-6, we outline run_inference, pull out hidden_dim and num_heads, and construct a listing of goal seq_lengths (1 to 101 in steps of 10), together with empty lists for kv_cache_sizes and inference_times.
On Traces 8-11, we initialize kv_cache with empty tensors for 'okay' and 'v' of form [1, num_heads//group_size, 0, head_dim] so it could possibly develop as we generate tokens.
Then, within the loop over every seq_len on Traces 13-17, we simulate feeding one random token x at a time into the transformer block, timing the ahead go, and updating kv_cache.
Lastly, on Traces 19-23, we measure the entire variety of components within the cached keys and values, append that to kv_cache_sizes, file the elapsed time to inference_times, after which return all three lists for plotting or evaluation.
Experiments and Evaluation
Lastly, we’ll check our implementation of grouped question consideration with totally different group sizes 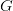 .
.
For every group dimension, we’ll plot the scale of the KV Cache and inference time as a perform of sequence size.
plt.determine(figsize=(12, 5))
plt.subplot(1, 2, 1)
for group_size in [1, 2, 4, 8, 16, 32]:
gqa_block = TransformerBlock(hidden_dim=4096, num_heads=32, group_size=group_size)
seq_lengths, sizes, instances = run_inference(gqa_block, group_size=group_size)
plt.plot(seq_lengths, sizes, label="GQA : {}".format(group_size))
plt.xlabel("Generated Tokens")
plt.ylabel("KV Cache Dimension")
plt.title("KV Cache Progress")
plt.legend()
plt.subplot(1, 2, 2)
for group_size in [1, 2, 4, 8, 16, 32]:
gqa_block = TransformerBlock(hidden_dim=4096, num_heads=32, group_size=group_size)
seq_lengths, sizes, instances = run_inference(gqa_block, group_size=group_size)
plt.plot(seq_lengths, instances, label="GQA : {}".format(group_size))
plt.xlabel("Generated Tokens")
plt.ylabel("Inference Time (s)")
plt.title("Inference Velocity")
plt.legend()
plt.tight_layout()
plt.present()
On Traces 1 and a pair of, we arrange a 12×5-inch determine and declare the primary subplot for KV cache development.
Between Traces 4-7, we loop over numerous group_size values, instantiate a TransformerBlock for every, name run_inference to assemble sequence lengths and cache sizes, and plot the KV cache dimension versus the variety of generated tokens.
On Traces 14-18, we change to the second subplot, repeat the loop to gather and plot inference instances towards token counts, and at last, on Traces 21-28, we set axis labels, add a title and legend, tighten the structure, and name plt.present() to render each charts (Determine 4).
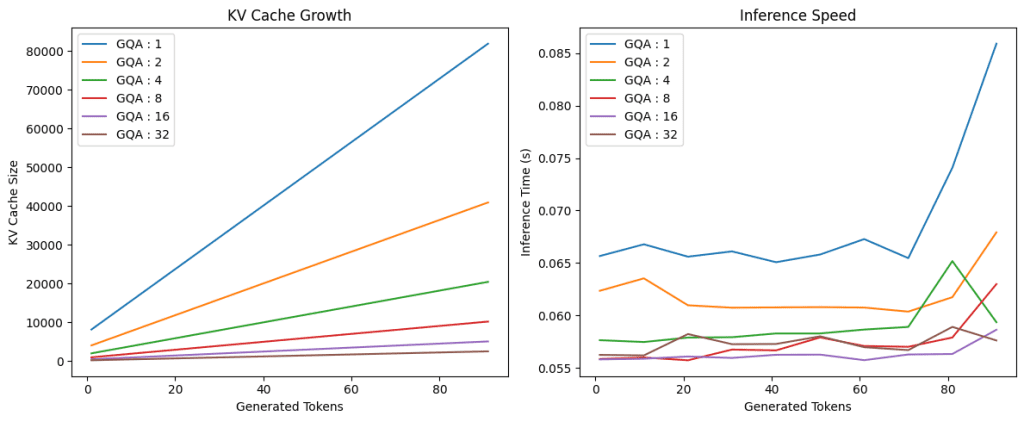
As proven in Determine 4, utilizing grouped question consideration considerably reduces the KV cache dimension and inference time in comparison with vanilla multihead self-attention (group dimension 1).
What’s subsequent? We suggest PyImageSearch College.
86+ whole courses • 115+ hours hours of on-demand code walkthrough movies • Final up to date: October 2025
★★★★★ 4.84 (128 Scores) • 16,000+ College students Enrolled
I strongly imagine that when you had the fitting trainer you could possibly grasp pc imaginative and prescient and deep studying.
Do you suppose studying pc imaginative and prescient and deep studying needs to be time-consuming, overwhelming, and sophisticated? Or has to contain advanced arithmetic and equations? Or requires a level in pc science?
That’s not the case.
All you must grasp pc imaginative and prescient and deep studying is for somebody to elucidate issues to you in easy, intuitive phrases. And that’s precisely what I do. My mission is to alter training and the way advanced Synthetic Intelligence subjects are taught.
Should you’re critical about studying pc imaginative and prescient, your subsequent cease must be PyImageSearch College, probably the most complete pc imaginative and prescient, deep studying, and OpenCV course on-line immediately. Right here you’ll discover ways to efficiently and confidently apply pc imaginative and prescient to your work, analysis, and tasks. Be a part of me in pc imaginative and prescient mastery.
Inside PyImageSearch College you will discover:
- &examine; 86+ programs on important pc imaginative and prescient, deep studying, and OpenCV subjects
- &examine; 86 Certificates of Completion
- &examine; 115+ hours hours of on-demand video
- &examine; Model new programs launched repeatedly, guaranteeing you’ll be able to sustain with state-of-the-art strategies
- &examine; Pre-configured Jupyter Notebooks in Google Colab
- &examine; Run all code examples in your net browser — works on Home windows, macOS, and Linux (no dev surroundings configuration required!)
- &examine; Entry to centralized code repos for all 540+ tutorials on PyImageSearch
- &examine; Simple one-click downloads for code, datasets, pre-trained fashions, and so forth.
- &examine; Entry on cell, laptop computer, desktop, and so forth.
Abstract
We start by framing the problem of lengthy‐context inference in transformer fashions. As sequence lengths develop, storing previous key and worth tensors within the KV cache turns into a significant reminiscence and bandwidth bottleneck. To deal with this, we introduce Grouped Question Consideration (GQA), an architectural modification that permits a number of question heads to share a smaller set of key-value heads, thereby decreasing the cache footprint with minimal impression on accuracy.
Subsequent, we unpack the mechanics of KV caching — why transformers retailer per‐head key and worth sequences, how cache dimension scales with head depend 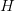 , context size
, context size 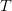 , and mannequin depth
, and mannequin depth 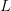 , and the ensuing latency strain from studying giant caches every token. We then formally outline GQA, displaying how the grouping issue
, and the ensuing latency strain from studying giant caches every token. We then formally outline GQA, displaying how the grouping issue 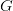 reduces the variety of KV projections from
reduces the variety of KV projections from 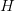 to
to 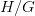 and yields a
and yields a 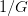 discount in cache reminiscence. We illustrate this with equations and intuitive diagrams, contrasting vanilla multi‐head consideration, multi‐question consideration, and the GQA center floor.
discount in cache reminiscence. We illustrate this with equations and intuitive diagrams, contrasting vanilla multi‐head consideration, multi‐question consideration, and the GQA center floor.
Lastly, we stroll via a hands-on implementation: constructing a toy TransformerBlock in PyTorch that helps arbitrary GQA groupings, wiring up KV cache development, and operating inference experiments throughout group sizes. We plot how cache dimension and per-token inference time evolve for  , analyze the memory-latency trade-off, and distill sensible tips for selecting
, analyze the memory-latency trade-off, and distill sensible tips for selecting 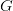 and integrating GQA into real-world LLM deployments.
and integrating GQA into real-world LLM deployments.
Quotation Info
Mangla, P. “Introduction to KV Cache Optimization Utilizing Grouped Question Consideration,” PyImageSearch, P. Chugh, S. Huot, A. Sharma, and P. Thakur, eds., 2025, https://pyimg.co/b241m
@incollection{Mangla_2025_intro-to-kv-cache-optimization-using-grouped-query-attention,
writer = {Puneet Mangla},
title = {{Introduction to KV Cache Optimization Utilizing Grouped Question Consideration}},
booktitle = {PyImageSearch},
editor = {Puneet Chugh and Susan Huot and Aditya Sharma and Piyush Thakur},
12 months = {2025},
url = {https://pyimg.co/b241m},
}
To obtain the supply code to this submit (and be notified when future tutorials are printed right here on PyImageSearch), merely enter your e mail tackle within the type under!

Obtain the Supply Code and FREE 17-page Useful resource Information
Enter your e mail tackle under to get a .zip of the code and a FREE 17-page Useful resource Information on Laptop Imaginative and prescient, OpenCV, and Deep Studying. Inside you will discover my hand-picked tutorials, books, programs, and libraries that can assist you grasp CV and DL!
The submit Introduction to KV Cache Optimization Utilizing Grouped Question Consideration appeared first on PyImageSearch.