Just a few days in the past I wrote two posts about how one can create a Smith chart, a graphical machine used for impedance calculations. Then somebody emailed me to level out the connection between the Smith chart and triangular numbers.
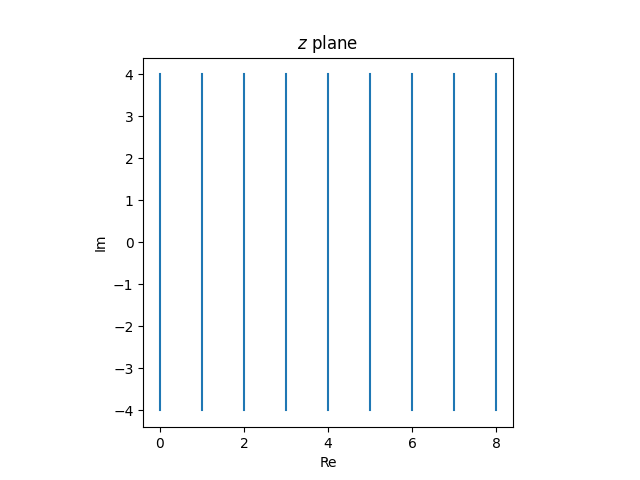
The Smith chart is the picture of an oblong grid in the precise half-plane below the operate
f(z) = (z − 1)/(z + 1).
For those who subtract the values of f at consecutive integers, you get the reciprocal of a triangular quantity.
f(n) − f(n − 1) = 2/(n(n + 1)) = 1 / Tn
Or to place it one other method,
f(n) − f(n − 1) = 1 / (1 + 2 + 3 + … + n).
Within the first put up on the Smith chart we confirmed that the operate f maps vertical strains
within the z aircraft to circles within the w aircraft all touching at w = 1.
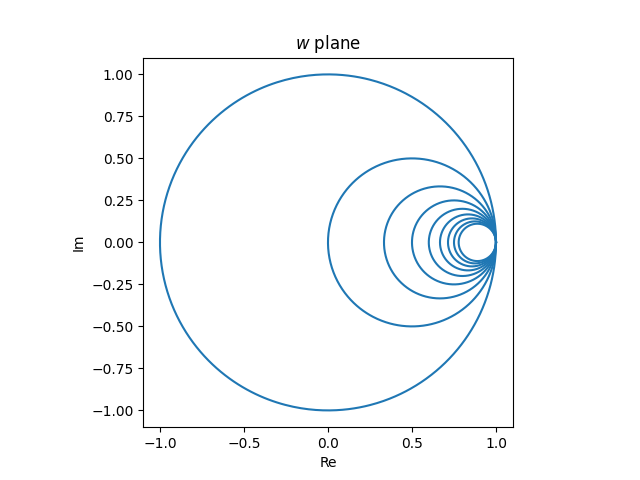
The circles are symmetric about the actual axis and the diameter runs from f(n) to 1. The separation between the circles on the left facet is thus
f(n) − f(n − 1) = 1 / Tn.
Quantity the circles ranging from the outermost as 0, 1, 2, …. Then the utmost distance between circle n and circle n − 1 is 1 / Tn. You’ll be able to see within the graph above that the gap between circle 0 and circle 1 is 1. It’s just a little tougher to see that the gap between circle 1 and circle 2 is 1/3. It seems like the gap between circles 2 and three is about half of that between circles 1 and a couple of, so it will be 1/6.
Associated posts