The weblog accommodates fundamentals of strip plot design, randomization, ANOVA mannequin, all of the formulation and solved instance together with demonstration in Agri Analyze. (Studying time 15 min.)
The Strip Plot Design (SPD) is
significantly appropriate for two-factor experiments the place increased precision is
wanted for measuring the interplay impact between the components in comparison with
measuring the principle results of both issue individually. This design can also be
splendid when each units of remedies require massive plots. For example, in
experiments involving spacing and ploughing remedies, cultural comfort
necessitates bigger plots. Ploughing strips will be organized in a single path,
and spacing strips will be laid out perpendicular to the ploughing strips. This
association is achieved utilizing:
- Vertical strip plot for the primary issue (the vertical
issue) - Horizontal strip plot for the second issue (the
horizontal issue) - Interplay plot for the interplay between the 2
components.
The vertical and horizontal strip plots are
at all times perpendicular to one another. Nevertheless, their sizes are unrelated, in contrast to
the principle plot and subplot within the break up plot design. The interplay plot is the
smallest. In a strip plot design, the precision of the principle results of each
components is sacrificed to enhance the precision of the interplay impact.
Randomization and Structure Planning for Strip Plot
Design
Step
1: Assign horizontal plots by dividing the
experimental space into r blocks, then dividing every block into horizontal
strips. Comply with the randomization process utilized in RBD, and randomly assign the
ranges of the primary issue to the horizontal strips inside every of the r
blocks, individually and independently.
Step
2: Assign vertical plots by dividing every
block into b vertical strips. Comply with the randomization process utilized in RBD
with b remedies and r replications, and randomly assign the b ranges to the
vertical strips inside every block, individually and independently.
Structure Instance:
A pattern structure of strip-plot design with six varieties (V1, V2, V3, V4, V5 and V6) as a horizontal issue and three nitrogen charges (N1, N2 and N3) as a vertical think about three replications.
Instance
of Strip Plot Design
Within the earlier chapter, this dataset
was used for a split-plot design and now the identical dataset might be used to
illustrate a strip plot design.
A strip plot
design was used to research the results of irrigation ranges (Horizontal
issue) and fertilizer sorts (Vertical issue) on the yield of a specific
crop. The experiment was carried out over 4 replicates (R1, R2, R3, R4).
Elements:
Horizontal Issue (A – Irrigation
Ranges):
A1: Low Irrigation
A2: Medium Irrigation
A3: Excessive Irrigation
Vertical Issue (B – Fertilizer
Sorts):
B1: Natural Fertilizer
B2: Inorganic Fertilizer
B3: Combined Fertilizer
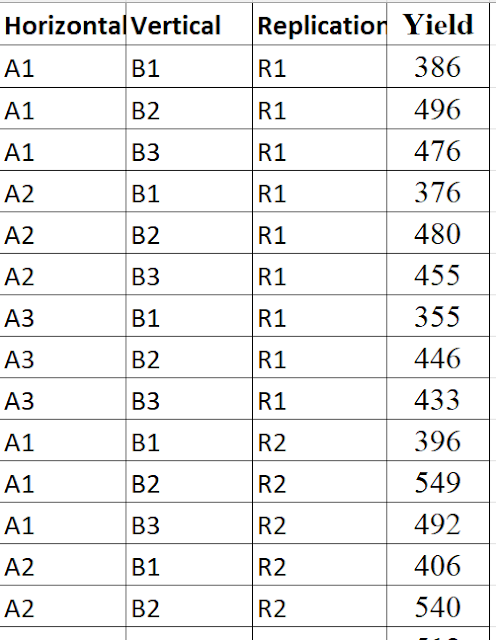
|
Remedies |
R1 |
R2 |
R3 |
R4 |
|
A1B1 |
386 |
396 |
298 |
387 |
|
A1B2 |
496 |
549 |
469 |
513 |
|
A1B3 |
476 |
492 |
436 |
476 |
|
A2B1 |
376 |
406 |
280 |
347 |
|
A2B2 |
480 |
540 |
436 |
500 |
|
A2B3 |
455 |
512 |
398 |
468 |
|
A3B1 |
355 |
388 |
201 |
337 |
|
A3B2 |
446 |
533 |
413 |
482 |
|
A3B3 |
433 |
482 |
334 |
435 |
Closing ANOVA Desk for Crop Yield
Evaluation Utilizing Strip Plot Design with Irrigation and Fertilizer Remedies:
|
|
TABLE F |
|||||
|
SV |
DF |
SS |
MS |
CAL F |
5% |
1% |
|
Replication |
3 |
61636.97 |
20545.66 |
28.12 |
3.49 |
10.80 |
|
Horizontal plot (A) |
2 |
12391.17 |
6195.58 |
8.48 |
5.14 |
10.92 |
|
Error (A) |
6 |
4382.61 |
730.44 |
|
|
|
|
Vertical Plot (B) |
2 |
128866.67 |
64433.33 |
81.35 |
5.14 |
10.92 |
|
Error (B) |
6 |
4752.44 |
792.07 |
|
|
|
|
A X B |
4 |
304.17 |
76.04 |
0.62 |
3.26 |
5.41 |
|
Error (C) |
12 |
1462.72 |
121.89 |
|
|
|
|
Whole |
35 |
213796.75 |
|
|
|
|
Calculation of levels of freedom:
Replication DF: r-1 = 4-1=3
Fundamental plot (A): a-1=3-1=2
Error (A): (r-1)*(a-1)=3*2=6
Fundamental plot (B): b-1=3-1=2
Error (B): (r-1)*(b-1)=3*2=6
A x B: (a-1)*(b-1)=2*2=4
Error (C): (r-1)*(a-1)*(b-1)=3*2*2=12
Whole: rab-1=4*3*3-1=35
Calculation of MS:
Replication:
61636.97/3=20545.66
Fundamental
plot (A): 12391.17/2=6195.58
Error
(A): 4382.61/6=730.44
Fundamental
plot (B): 128866.67/2=64433.33
Error
(B): 4752.44/6=792.07.
A
x B: 304.17/4=76.04
Error
(C): 1462.72/12=121.89
Conclusion:
·
The calculated F-value (28.12) is far better than the essential
F-values at each 5% (3.49) and 1% (10.80) significance ranges. Due to this fact,
there may be sturdy proof to recommend that there are vital variations
between the replicates.
·
The calculated F-value (8.48) for horizontal issue exceeds the
essential F-value 5% (5.14) significance ranges. This means that there are vital
variations among the many irrigation degree.
·
The calculated F-value (81.35) for vertical issue exceeds the essential
F-value at 1% (10.92) significance degree. This means that there’s extremely
vital variation amongst degree of fertilizer.
·
The calculated F-value (0.62) for interplay between fundamental issue and
sub issue (A x B) which is lower than essential F-value at 5% (2.93)
significance degree. This point out that there’s non-significant interplay
between irrigation and fertilizer.
·
For the irrigation, highest yield was noticed for A1 and A2 have been discovered
statistically at par with it based mostly on essential distinction.
·
For the fertilizer, highest yield was noticed for B2 and not one of the
degree of fertilizer at par with it based mostly on essential distinction.
Steps to carry out evaluation of break up plot design in
Agri Analyze
Step 1: To create a CSV file with columns for replication,
Horizontal issue (A), vertical issue (B) and Yield. Hyperlink of the dataset
Step 2: Go together with Agri Analyze website https://agrianalyze.com/Default.aspx
Step 3: Click on on ANALYTICAL TOOL
Step 4: Click on on DESIGN OF EXPERIMENT
Step 5: Click on on STRIP PLOT DESIGN ANALYSIS
Step6: Choose CSV file
Step 7: Choose Replication, Horizontal issue (A), Vertical issue (B) and Dependent variable (Yield)
Step 8: Choose a check for a number of comparisons, akin to Least Vital Distinction (LSD) check or Tuckey’s check or Duncan’s New A number of Vary Take a look at (DNMRT check) for grouping of remedy means.
Step 10: After submit
obtain evaluation report.
Output Consequence
REFERENCES
Gomez, Okay. A., & Gomez, A. A. (1984). Statistical Procedures for Agricultural Analysis. John wiley & sons. 108-120.
This weblog is written by:
Content material Author
Agri Analyze