Suppose f(x) is the sum of phrases of the shape cos(kx) the place okay is an integer from a set A with n parts.
Then the utmost worth of f is f(0) = n. However what’s the minimal worth of f?
The Chowla cosine conjecture says that the minimal must be lower than −√n for giant n. For now one of the best confirmed outcomes are a lot smaller in absolute worth [1].
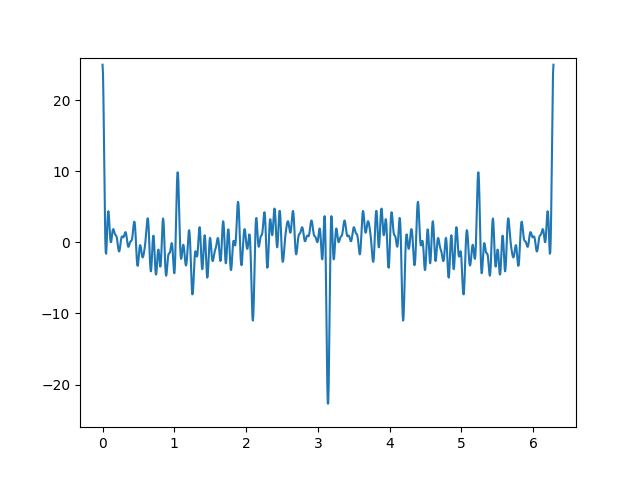
I used to be taking part in round with this drawback, and the very first thing I considered was to let the set A be the primary n primes. This turned out to not be essentially the most attention-grabbing instance. Since all of the primes aside from the primary are odd, and cos(okayπ) = −1 for odd okay, the minimal was all the time roughly −n and all the time occurred close to π [2].
Right here’s a plot the place A is the set of primes lower than 100.
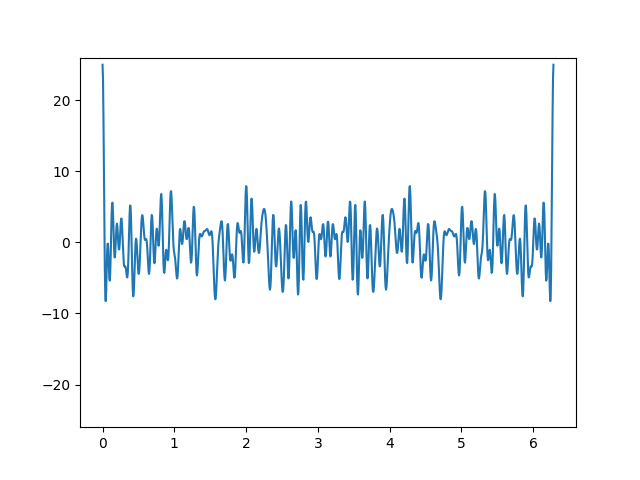
For the cosine conjecture to be attention-grabbing, the set A ought to include a mixture of even and odd numbers.
Right here’s a plot with A equal to a random choice of 25 factors between 1 and 100. (I selected 25 as a result of there are 25 primes lower than 100.)
Right here’s the Python code I used to generate the 2 units A and the perform to plot.
import numpy as np
from sympy import prime
def f(x, A):
return sum([np.cos(k*x) for k in A])
n = 25
A_prime = [prime(i) for i in range(1, n+1)]
np.random.seed(20260207)
A_random = np.random.alternative(vary(1, 101), measurement=n, change=False)
In case you wished to discover the Chowla conjecture numerically, direct use of minimization software program is impractical. As you may inform from the plots above, there are lots of native minima. If the values in A aren’t too massive, you may have a look at a plot to see roughly the place the minimal happens, then use a numerical methodology to search out the minimal on this area, however that doesn’t scale.
Right here’s an strategy that will scale higher. You possibly can discover all of the zeros of the by-product of fA and consider the perform at every. Certainly one of these is the minimal. The by-product is a sum of sines with integer frequencies, and so it could possibly be written as a polynomial in z = exp(ix) [3]. You possibly can discover all of the zeros of this polynomial utilizing the QR algorithm as mentioned within the earlier publish.
[1] Benjamin Bedert. Polynomial bounds for the Chowla cosine drawback. arXiv
[2] If A is the set of the primary n primes, fA(π) = 2 − n as a result of the sum defining fA(π) has one time period equal to 1 and n − 1 phrases equal to −1. I feel for n ≥ 4 that is the minimal, however I haven’t verified this. If that’s the case, the minimal isn’t simply close to π however precisely at π.
[3] You get a polynomial of diploma n in z and 1/z. Then multiply by z2n to get a polynomial in z solely of diploma 2n.
