If the earth had been an ideal sphere, “down” can be the path to the middle of the earth, wherever you stand. However as a result of our planet is a bit flattened on the poles, a line perpendicular to the floor and a line to the middle of the earth should not the identical. They’re practically the identical as a result of the earth is sort of a sphere, however not precisely, until you’re on the equator or at one of many poles. Typically the distinction issues and typically it doesn’t.
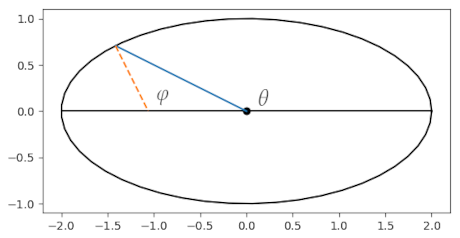
From a given level on the earth’s floor, draw two strains: one straight down (i.e. perpendicular to the floor) and one straight to the middle of the earth. The angle φ that the previous makes with the equatorial aircraft is geographic latitude. The angle θ that the latter makes with the equatorial aircraft is geocentric latitude.
For illustration we’ll draw an ellipse that’s much more eccentric than a polar cross-section of the earth.
At first it will not be clear why geographic latitude is outlined the best way it’s; geocentric latitude is conceptually easier. However geographic latitude is less complicated to measure: a plumb bob will present you which of them path is straight down.
There could also be some slight variation between the path of a plumb bob and a perpendicular to the earth’s floor resulting from variations in floor gravity. Nevertheless, the deviations resulting from gravity are a pair orders of magnitude smaller than the variations between geographic and geocentric latitude.
Conversion formulation
The conversion between the 2 latitudes is as follows.
Right here e is eccentricity. The equations above work for any elliipsoid, however for earth particularly e² = 0.00669438.
The perform atan2(y, x) returns an angle in the identical quadrant as the purpose (x, y) whose tangent is y/x. [1]
As a fast sanity verify on the equations, word that when eccentricity e is zero, i.e. within the case of a circle, φ = θ. Additionally, if φ = 0 then θ = φ for all eccentricity values.
Subsequent we give a proof of the equations above.
Proof
We are able to parameterize an ellipse with semi-major axis a and semi-minor axis b by
The slope at some extent (x(t), y(t)) is the ratio
and so the slope of a line perpendicular to the tangent, i.e tan φ, is
Now
and so
the place e² = 1 − b²/a² is the eccentricity of the ellipse. Due to this fact
and the equations on the prime of the put up comply with.
Distinction
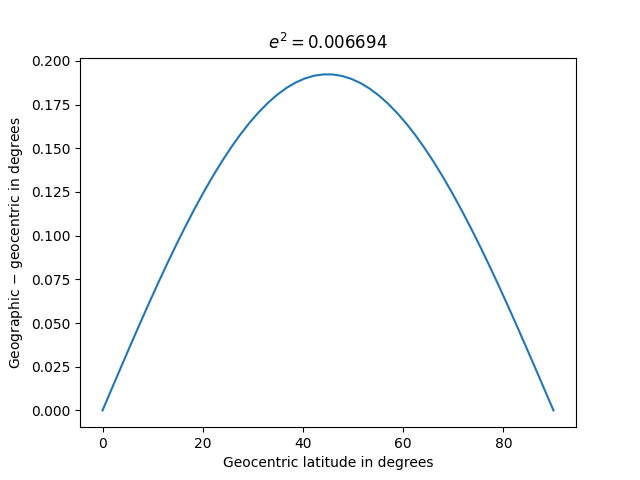
For the earth’s form, e² = 0.006694 per WGS84. For small eccentricities, the distinction between geographic and geocentric latitude is roughly symmetric round 45°.
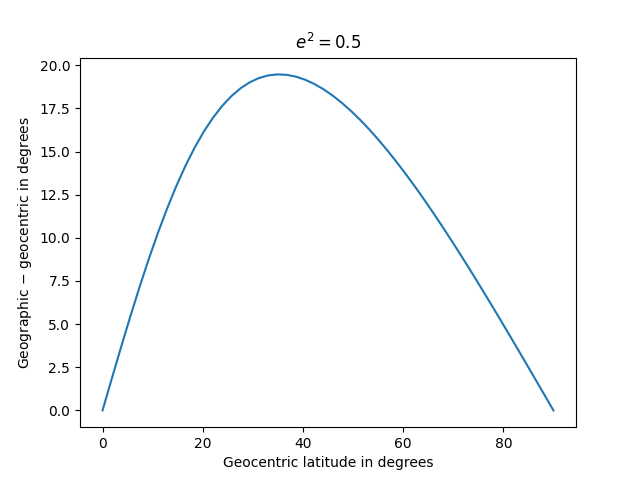
However for bigger values of eccentricity the asymmetry turns into extra pronounced.
Associated posts
[1] There are a pair problems with programming language implementations of atan2. Some name the perform arctan2 and a few reverse the order of the arguments. Extra on that right here.