This put up is written with my PhD pupil and now visitor creator Patrik Reizinger and is an element 4 of a sequence of posts on causal inference:
A technique to consider causal inference is that causal fashions require a extra fine-grained fashions of the world in comparison with statistical fashions. Many causal fashions are equal to the identical statistical mannequin, but help completely different causal inferences. This put up elaborates on this level, and makes the connection between causal and statistical fashions extra exact.
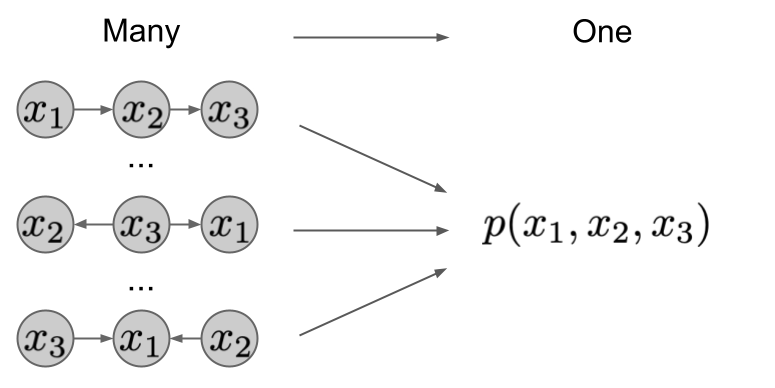
Do you keep in mind these combinatorics issues from college the place the query was what number of methods exist to get from a begin place to a goal subject on a chessboard? And you’ll solely transfer one step proper or one step down. When you keep in mind, then I have to admit that we are going to not take into account issues like that. However its (one doable) takeaway truly might help us to grasp Markov factorizations.
You already know, it’s completely detached the way you traversed the chessboard, the consequence is identical. So we will say that – from the attitude of goal place and the method of getting there – it is a many-to-one mapping. The identical holds for random variables and causal generative fashions.
If in case you have a bunch of random variables – let’s name them $X_1, X_2, dots, X_n$ -, their joint distribution is $p left(X_1, X_2, dots, X_n proper) $. When you invoke the chain rule of likelihood, you should have a number of choices to precise this joint as a product of things:
$$
p left(X_1, X_2, dots, X_n proper) = prod p(X_{pi_i}vert X_{pi_1}, ldots, X_{pi_{i-1}}),
$$
the place $pi_i$ is a permutation of indices. Since you are able to do this for any permutation $pi$, the mapping between such factorizations and the joint distribution they categorical is many-to-one. As you’ll be able to see this within the picture under. The completely different factorizations induce a unique graph, however have the identical joint distribution.
Since you might be studying this put up, you could already bear in mind that in causal inference we frequently speak about a causal factorization, which appears to be like like
$$
p left(X_1, X_2, dots, X_n proper) = prod_{i=1}^{n} pleft(X_i | X_{mathrm{pa}(i)}proper),
$$
the place $mathrm{pa}(X_i)$ denotes the causal dad and mom of node $X_i$. That is one in every of many doable methods you’ll be able to factorize the joint distribution, however we take into account this one particular. Within the current work, Schölkopf et al. name it a disentangled mannequin. What are disentangled fashions? Disentangled components describe unbiased features of the mechanism that generated the info. And they aren’t unbiased since you factored them on this manner, however you had been searching for this factorization as a result of its components are unbiased.
In different phrases, for each joint distribution there are numerous doable factorizations, however we assume that just one, the causal or disentangled factorization, describes the true underlying course of that generated the info.
Let’s take into account an instance for disentangled fashions. We wish to mannequin the joint distribution of altitude $A$ and temperature $T$. On this case, the causal route is $A rightarrow T$ – if the altitude adjustments, the distribution of the temperature will change too. However you can not change the altitude by artificially heating a metropolis – in any other case all of us would get pleasure from views as in Miami; world warming is actual however luckily has no altitude-changing impact.
Ultimately, we get the factorization of $p(A)p(T|A)$. The necessary insights listed below are the solutions to the query: What will we count on from these components? The previously-mentioned Schölkopf et al. paper calls the primary takeaway the Impartial Causal Mechanisms (ICM) Precept, i.e.
By conditioning on the dad and mom of any issue within the disentangled mannequin, the issue will neither have the ability to provide you with additional details about different components nor is ready to affect them.
Within the above instance, which means in case you take into account completely different nations with their altitude distributions, you’ll be able to nonetheless use the identical $p(T|A),$ i.e., the components generalize nicely. For no affect, the instance holds straight above the ICM Precept. Moreover, figuring out any of the components – e.g. $p(A)$ – will not inform something in regards to the different (no info). If you already know which nation you might be in, so can have no clue in regards to the local weather (in case you consulted the web site of the corresponding climate company, that is what I name dishonest). Within the different route, regardless of being the top-of-class pupil in local weather issues, you will not have the ability to inform the nation if any person says to you that right here the altitude is 350 meters and the temperature is 7°C!
Statistical vs causal inference
We mentioned Markov factorizations, as they assist us perceive the philosophical distinction between statistical and causal inference. The sweetness, and a supply of confusion, is that one can use Markov factorizations in each paradigms.
Nonetheless, whereas utilizing Markov factorizations is elective for statistical inference, it’s a should for causal inference.
So why would a statistical inference individual use Markov factorizations? As a result of they make life simpler within the sense that you do not want to fret about too excessive electricty prices. Particularly, factorized fashions of knowledge may be computationally rather more environment friendly. As an alternative of modeling a joint distribution straight, which has a whole lot of parameters – within the case of $n$ binary variables, that’s $2^n-1$ completely different values -, a factorized model may be fairly light-weight and parameter-efficient. If you’ll be able to factorize the joint in a manner that you’ve 8 components with $n/8$ variables every, then you’ll be able to describe your mannequin with $8times2^{n/8}-1$ parameters. If $n=16$, that’s $65,535$ vs $31$. Equally, representing your distibution in a factorized kind offers rise to environment friendly, general-purpose message-passing algorithms, akin to perception propagation or expectation propagation.
However, causal inference folks actually need this, in any other case, they’re misplaced. As a result of with out Markov factorizations, they can’t actually formulate causal claims.
A causal practicioner makes use of Markov factorizations, as a result of this fashion she is ready to motive about interventions.
When you don’t have the disentangled factorization, you can not mannequin the impact of interventions on the actual mechanisms that make the system tick.
Connection to area adaptation
In plain machine studying lingo, what you wish to do is area adaptation, that’s, you wish to draw conclusions a couple of distribution you didn’t observe (these are the interventional ones). The Markov factorization prescribes methods wherein you count on the distribution to alter – one issue at a time – and thus the set of distributions you need to have the ability to robustly generalise to or draw inferences about.
Do calculus
Do-caclculus, the subject of the first put up within the sequence, may be comparatively merely described utilizing Markov factorizations. As you keep in mind, $mathrm{do}(X=x)$ implies that we set the variable $X$ to the worth $x$, which means that the distribution of that variable $p(X)$ collapses to a degree mass. We are able to mannequin this intervention mathematically by changing the issue $p( x vert mathrm{pa}(X))$ by a Dirac-delta $delta_x$, ensuing within the deletion of all incoming edges of the intervened components within the graphical mannequin. We then marginalise over $x$ to calculate the joint distribution of the remaining variables. For instance, if we’ve got two variables $x$ and $y$ we will write:
$$
p(yvert do(X=x_0)) = int p(x,y) frac{delta(x – x_0)}{p(xvert y)} dx
$$
SEMs, Markov factorization, and the reparamtrization trick
When you’ve learn the earlier components on this sequence, you will know that Markov factorizations aren’t the one software we use in causal inference. For counterfactuals, we used structural equation fashions (SEMs). On this half we are going to illustrate the connection between these with a tacky reference to the reparametrization trick utilized in VAEs amongst others.
However earlier than that, let’s recap SEMs. On this case, you outline the connection between the kid node and its dad and mom by way of a practical project. For node $X$ with dad and mom $mathrm{pa}(X)$ it has the type of
$$
X = f(mathrm{pa}(X), epsilon),
$$
with some noise $epsilon.$ Right here, you must learn “=” within the sense of an assigment (like in Python), in arithmetic, this ought to be “:=”.
The above equation expresses the conditional likelihood $ pleft(X| mathrm{pa}(X)proper)$ as a deterministic operate of $X$ and a few noise variable $epsilon$. Wait a second…, is not it the identical factor what the reparametrization trick does? Sure it’s.
So the SEM formulation (referred to as the implicit distribution) is expounded by way of the reparametrization trick to the conditional likelihood of $X$ given its dad and mom.
Lessons of causal fashions
Thus, we will say {that a} SEM is a conditional distribution, and vica versa. Okay, however how do the units of those constructs relate to one another?
If in case you have a SEM, then you’ll be able to learn off the conditional, which is distinctive. However, yow will discover extra SEMs for a similar conditional. Simply as you’ll be able to categorical a conditional distribution in a number of other ways utilizing completely different reparametrizations, it’s doable to precise the identical Markov factorization by a number of SEMs. Think about for instance that in case your distribution is $mathcal{N}(mu,sigma),$ then multiplying it by -1 offers you a similar distribution. On this sense, SEMs are a richer class of fashions than Markov factorizations, thus they permit us to make inferences (counterfactual) which we weren’t capable of categorical within the extra coarse grained language of Markov Factorizations.
As we mentioned above, a single joint distribution has a number of legitimate Markov factorizations, and the identical Markov factorization may be expressed as completely different SEMs. We are able to consider joint distributions, Markov factorizations, and SEMs as more and more fine-grained mannequin lessons: joint distributions $subset$ Markov facorizations $subset$ SEMs. The extra features of the info producing course of you mannequin, the extra elaborate the set of inferences you can also make change into. Thus, Joint distributions will let you make predictions underneath no mechanism shift, Markov factorizations will let you mannequin interventions, SEMs will let you make counterfactual statements.
The worth you pay for extra expressive fashions is that additionally they get typically a lot tougher to estimate from knowledge. In truth, some features of causal fashions are unimaginable to deduce from i.i.d. observational knowledge. Furthermore, some counterfactual inferences are experimentally not verifiable.