In my final two posts, I confirmed you learn how to calculate energy for a t check utilizing Monte Carlo simulations and learn how to combine your simulations into Stata’s energy command. In immediately’s put up, I’m going to indicate you learn how to do these duties for linear and logistic regression fashions. The technique and general construction of the applications for linear and logistic regression are much like the t check examples. The elements that may change are the simulation of the info and the fashions used to check the null speculation.
Selecting sensible regression parameters is difficult when simulating regression fashions. Typically, pilot knowledge or historic knowledge can present clues, however typically we should contemplate a variety of parameter values that we imagine are sensible. I’m going to take care of this problem by working examples which might be primarily based on the info from the Nationwide Well being and Vitamin Examination Survey (NHANES). You’ll be able to obtain a model of those knowledge by typing webuse nhanes2.
Linear regression instance
Let’s think about that you’re planning a research of systolic blood strain (SBP) and also you imagine that there’s an interplay between age and intercourse. The NHANES dataset contains the variables bpsystol (SBP), age, and intercourse. Under, I’ve match a linear regression mannequin that features an age-by-sex interplay time period, and the p-values for all of the parameter estimates equal 0.000. This isn’t shocking, as a result of the dataset contains 10,351 observations. p-values turn into smaller as pattern sizes turn into bigger when all the things else is held fixed.
. webuse nhanes2
. regress bpsystol c.age##ib1.intercourse
Supply | SS df MS Variety of obs = 10,351
-------------+---------------------------------- F(3, 10347) = 1180.87
Mannequin | 1437147 3 479049 Prob > F = 0.0000
Residual | 4197523.03 10,347 405.675367 R-squared = 0.2551
-------------+---------------------------------- Adj R-squared = 0.2548
Whole | 5634670.03 10,350 544.412563 Root MSE = 20.141
------------------------------------------------------------------------------
bpsystol | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .47062 .0167357 28.12 0.000 .4378147 .5034252
|
intercourse |
Feminine | -20.45813 1.165263 -17.56 0.000 -22.74227 -18.17398
|
intercourse#c.age |
Feminine | .3457346 .0230373 15.01 0.000 .300577 .3908923
|
_cons | 110.5691 .8440692 131.00 0.000 108.9146 112.2236
------------------------------------------------------------------------------
Maybe you don’t have the sources to gather a pattern of 10,351 contributors to your research, however you wish to have 80% energy to detect an interplay parameter of 0.35. How massive does your pattern have to be?
Let’s begin by making a single pseudo-random dataset primarily based on the parameter estimates from the NHANES mannequin. We start the code block under by clearing Stata’s reminiscence. Subsequent, we set the random seed to fifteen in order that we will reproduce our outcomes and set the variety of observations to 100.
clear set seed 15 set obs 100 generate age = runiformint(18,65) generate feminine = rbinomial(1,0.5) generate work together = age*feminine generate e = rnormal(0,20) generate sbp = 110 + 0.5*age + (-20)*feminine + 0.35*work together + e
The fourth line of the code block generates a variable named age, which incorporates integers drawn from a uniform distribution on the interval [18,65].
The fifth line generates an indicator variable named feminine utilizing a Bernoulli distribution with chance equal to 0.5. Recall {that a} binomial distribution with one trial is equal to a Bernoulli distribution.
The sixth line generates a variable for the interplay of age and feminine.
The seventh line generates a variable, e, that’s the error time period for the regression mannequin. The errors are generated from a standard distribution with a imply of 0 and customary deviation of 20. The worth of 20 is predicated on the basis MSE estimated from the NHANES regression mannequin.
The final line of the code block generates the variable sbp primarily based on a linear mixture of our simulated variables and the parameter estimates from the NHANES regression mannequin.
Under are the outcomes of a linear mannequin match to our simulated knowledge utilizing regress. The parameter estimates differ considerably from our enter parameters as a result of I generated just one comparatively small dataset. We may cut back this discrepancy by rising our pattern dimension, drawing many samples, or each.
. regress sbp age i.feminine c.age#i.feminine
Supply | SS df MS Variety of obs = 100
-------------+---------------------------------- F(3, 96) = 7.15
Mannequin | 9060.32024 3 3020.10675 Prob > F = 0.0002
Residual | 40569.7504 96 422.601567 R-squared = 0.1826
-------------+---------------------------------- Adj R-squared = 0.1570
Whole | 49630.0707 99 501.313845 Root MSE = 20.557
------------------------------------------------------------------------------
sbp | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .7752417 .1883855 4.12 0.000 .4012994 1.149184
1.feminine | 5.759113 15.09611 0.38 0.704 -24.20644 35.72466
|
feminine#c.age |
1 | -.2690026 .3319144 -0.81 0.420 -.9278475 .3898423
|
_cons | 100.4409 8.381869 11.98 0.000 83.80306 117.0788
------------------------------------------------------------------------------
The p-value for the interplay time period equals 0.420, which isn’t statistically vital on the 0.05 stage. Clearly, we want a bigger pattern dimension.
We may use the p-value from the regression mannequin to check the null speculation that the interplay time period is zero. That will work on this instance as a result of we’re testing just one parameter. However we must check a number of parameters concurrently if our interplay included a categorical variable equivalent to race. And there could also be instances once we want to check a number of variables concurrently.
Chance-ratio checks can check many sorts of hypotheses, together with a number of parameters concurrently. I’m going to indicate you learn how to use a likelihood-ratio check on this instance as a result of it’s going to generalize to different hypotheses you could encounter in your analysis. You’ll be able to learn extra about likelihood-ratio checks within the Stata Base Reference Guide if you’re not accustomed to them.
The code block under exhibits 4 of the 5 steps used to calculate a likelihood-ratio check. We’ll check the null speculation that the coefficient for the interplay time period equals zero. The primary line matches the “full” regression mannequin that features the interplay time period. The second line shops the estimates of the total mannequin in reminiscence. The identify “full” is unfair. We may have named the outcomes of this mannequin something we like. The third line matches the “lowered” regression mannequin that omits the interplay time period. And the fourth line shops the outcomes of the lowered mannequin in reminiscence.
regress sbp age i.feminine c.age#i.feminine estimates retailer full regress sbp age i.feminine estimates retailer lowered
The fifth step makes use of lrtest to calculate a likelihood-ratio check of the total mannequin versus the lowered mannequin. The check yields a p-value of 0.4089, which is near the Wald check reported within the regression output above. We can’t reject the null speculation that the interplay parameter is zero.
. lrtest full lowered Chance-ratio check LR chi2(1) = 0.68 (Assumption: lowered nested in full) Prob > chi2 = 0.4089
You’ll be able to kind return listing to see that the p-value is saved within the scalar r(p). And you should utilize r(p) to outline reject the identical means we did in our t check program.
. return listing
scalars:
r(p) = .4089399864598747
r(chi2) = .6818803412616035
r(df) = 1
. native reject = (r(p)<0.05)
Simulating the info and testing the null speculation for a regression mannequin are a bit extra sophisticated than for a t check. However writing a program to automate this course of is nearly equivalent to the t check instance. Let’s contemplate the code block under, which defines this system simregress.
seize program drop simregress
program simregress, rclass
model 16
// DEFINE THE INPUT PARAMETERS AND THEIR DEFAULT VALUES
syntax, n(integer) /// Pattern dimension
[ alpha(real 0.05) /// Alpha level
intercept(real 110) /// Intercept parameter
age(real 0.5) /// Age parameter
female(real -20) /// Female parameter
interact(real 0.35) /// Interaction parameter
esd(real 20) ] // Commonplace deviation of the error
quietly {
// GENERATE THE RANDOM DATA
clear
set obs `n'
generate age = runiformint(18,65)
generate feminine = rbinomial(1,0.5)
generate work together = age*feminine
generate e = rnormal(0,`esd')
generate sbp = `intercept' + `age'*age + `feminine'*feminine + ///
`work together'*work together + e
// TEST THE NULL HYPOTHESIS
regress sbp age i.feminine c.age#i.feminine
estimates retailer full
regress sbp age i.feminine
estimates retailer lowered
lrtest full lowered
}
// RETURN RESULTS
return scalar reject = (r(p)<`alpha')
finish
The primary three traces, which start with seize program, program, and model, are principally the identical as in our t check program.
The syntax part of this system is much like that of the t check program, however the names of the enter parameters are, clearly, completely different. I’ve included enter parameters for the pattern dimension, alpha stage, and primary regression parameters. I’ve not included an enter parameter for each potential parameter within the mannequin, however you possibly can if you happen to like. For instance, I’ve “arduous coded” the vary of the variable age as 18 to 65 in my program. However you possibly can embody an enter parameter for the higher and decrease bounds of age if you want. I additionally discover it useful to incorporate feedback that describe the parameter names in order that there isn’t any ambiguity.
The following part of code is embedded in a “quietly” block. Instructions like set obs, generate, and regress ship output to the Outcomes window and log file (when you have one open). Putting these instructions in a quietly block suppresses that output.
Now we have already written the instructions to create our random knowledge and check the null speculation. So we will copy that code into the quietly block and change any enter parameters with their corresponding native macros outlined by syntax. For instance, I’ve modified set obs 100 to set obs `n’ in order that the variety of observations will likely be set by the enter parameter specified with syntax. I’ve additionally given the enter parameters the identical names because the simulated variables within the mannequin. So `age’*age is the product of the enter parameter `age’ outlined by syntax and the variable age generated by simulation.
The p-value from the likelihood-ratio check is saved within the scalar r(p), and our program returns the scalar reject precisely because it did in our t check program.
Under, I’ve used simulate to run simregress 100 instances and summarized the variable reject. The outcomes point out that we might have 16% energy to detect an interplay parameter of 0.35 given a pattern of 100 contributors and the opposite assumptions concerning the mannequin.
. simulate reject=r(reject), reps(100):
> simregress, n(100) age(0.5) feminine(20) work together(0.35)
> esd(20) alpha(0.05)
command: simregress, n(100) age(0.5) feminine(20) work together(0.35)
> esd(20) alpha(0.05)
reject: r(reject)
Simulations (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
. summarize reject
Variable | Obs Imply Std. Dev. Min Max
-------------+---------------------------------------------------------
reject | 100 .16 .3684529 0 1
Subsequent, let’s write a program known as power_cmd_simregress in order that we will combine simregress into Stata’s energy command. The construction of power_cmd_simregress is identical as power_cmd_ttest in my final put up. First, we outline the syntax and enter parameters and specify their default values. Then, we run the simulation and summarize the variable reject. And at last, we return the outcomes.
seize program drop power_cmd_simregress
program power_cmd_simregress, rclass
model 16
// DEFINE THE INPUT PARAMETERS AND THEIR DEFAULT VALUES
syntax, n(integer) /// Pattern dimension
[ alpha(real 0.05) /// Alpha level
intercept(real 110) /// Intercept parameter
age(real 0.5) /// Age parameter
female(real -20) /// Female parameter
interact(real 0.35) /// Interaction parameter
esd(real 20) /// Standard deviation of the error
reps(integer 100)] // Variety of repetitions
// GENERATE THE RANDOM DATA AND TEST THE NULL HYPOTHESIS
quietly {
simulate reject=r(reject), reps(`reps'): ///
simregress, n(`n') age(`age') feminine(`feminine') ///
work together(`work together') esd(`esd') alpha(`alpha')
summarize reject
}
// RETURN RESULTS
return scalar energy = r(imply)
return scalar N = `n'
return scalar alpha = `alpha'
return scalar intercept = `intercept'
return scalar age = `age'
return scalar feminine = `feminine'
return scalar work together = `work together'
return scalar esd = `esd'
finish
Let’s additionally write a program known as power_cmd_simregress_init. Recall from my final put up that this program will enable us to run energy simregress for a variety of enter parameter values, together with the parameters listed in double quotes.
seize program drop power_cmd_simregress_init
program power_cmd_simregress_init, sclass
sreturn native pss_colnames "intercept age feminine work together esd"
sreturn native pss_numopts "intercept age feminine work together esd"
finish
Now, we’re prepared to make use of energy simregress! The output under exhibits the simulated energy when the interplay parameter equals 0.2 to 0.4 in increments of 0.05 for samples of dimension 400, 500, 600, and 700.
. energy simregress, n(400(100)700) intercept(110) /// > age(0.5) feminine(-20) work together(0.2(0.05)0.4) /// > reps(1000) desk graph(xdimension(work together) /// > legend(rows(1))) Estimated energy Two-sided check +--------------------------------------------------------------------+ | alpha energy N intercept age feminine work together esd | |--------------------------------------------------------------------| | .05 .267 400 110 .5 -20 .2 20 | | .05 .398 400 110 .5 -20 .25 20 | | .05 .547 400 110 .5 -20 .3 20 | | .05 .677 400 110 .5 -20 .35 20 | | .05 .792 400 110 .5 -20 .4 20 | | .05 .33 500 110 .5 -20 .2 20 | | .05 .46 500 110 .5 -20 .25 20 | | .05 .646 500 110 .5 -20 .3 20 | | .05 .763 500 110 .5 -20 .35 20 | | .05 .854 500 110 .5 -20 .4 20 | | .05 .384 600 110 .5 -20 .2 20 | | .05 .563 600 110 .5 -20 .25 20 | | .05 .702 600 110 .5 -20 .3 20 | | .05 .841 600 110 .5 -20 .35 20 | | .05 .928 600 110 .5 -20 .4 20 | | .05 .444 700 110 .5 -20 .2 20 | | .05 .641 700 110 .5 -20 .25 20 | | .05 .793 700 110 .5 -20 .3 20 | | .05 .904 700 110 .5 -20 .35 20 | | .05 .958 700 110 .5 -20 .4 20 | +--------------------------------------------------------------------+
Determine 1 shows the outcomes graphically.
Determine 1: Estimated energy for the interplay time period in a regression mannequin
The desk and the graph present us that there are a number of combos of parameters that may end in 80% energy. A pattern of 700 contributors would give us roughly 80% energy to detect an interplay parameter of 0.30. A pattern of 600 contributors would give us roughly 80% energy to detect an interplay parameter of 0.33. A pattern of 500 contributors would give us roughly 80% energy to detect an interplay parameter of roughly 0.37. And a pattern of 400 contributors would give us roughly 80% energy to detect an interplay parameter of 0.40. Our remaining selection of pattern dimension is then primarily based on the dimensions of the interplay parameter that we wish to detect.
This instance targeted on the interplay time period in a regression mannequin with two covariates. However you possibly can modify this instance to simulate energy for nearly any sort of regression mannequin you’ll be able to think about. I’d recommend the next steps when planning your simulation:
- Write down the regression mannequin of curiosity, together with all parameters.
- Specify the small print of the covariates, such because the vary of age or the proportion of females.
- Find or take into consideration cheap values for the parameters in your mannequin.
- Simulate a single dataset assuming the choice speculation, and match the mannequin.
- Write a program to create the datasets, match the fashions, and use simulate to check this system.
- Write a program known as power_cmd_mymethod, which lets you run your simulations with energy.
- Write a program known as power_cmd_mymethod_init in an effort to use numlists for all parameters.
Let’s do this method for a logistic regression mannequin.
Logistic regression instance
On this instance, let’s think about that you’re planning a research of hypertension (highbp). Hypertension is binary, so we are going to use logistic regression to suit the mannequin and use odds ratios for the impact dimension.
Step 1: Write down the mannequin
Step one towards simulating energy is to write down down the mannequin.
[
{rm logit}({bf highbp}) = beta_0 + beta_1({bf age}) + beta_2({bf sex}) + beta_3({bf age}times {bf sex})
]
We might want to create variables for highbp, age, intercourse, and the interplay time period age(instances )intercourse. We may even must specify cheap parameter values for (beta_0), (beta_1), (beta_2), and (beta_3).
Step 2: Specify particulars of the covariates
Subsequent, we want to consider the covariates in our mannequin. What values of age are cheap for our research? Are we considering older adults? Youthful adults? Let’s assume that we’re considering adults between the ages of 18 and 65. Is the distribution of age prone to be uniform over the interval [18,65], or will we count on a hump-shaped distribution across the center of the age vary? We additionally want to consider the proportion of women and men in our research. Are we prone to pattern 50% males and 50% females? These are the sorts of questions that we have to ask ourselves when planning our energy calculations.
Let’s assume that we’re considering adults between the ages of 18 and 65 and we imagine that age is uniformly distributed. Let’s additionally assume that the pattern will likely be 50% feminine. The interplay time period age(instances )intercourse is simple to calculate as soon as we create variables for age and intercourse.
Step 3: Specify cheap values for the parameters
Subsequent we want to consider cheap values for the parameters in our mannequin. We may select parameter values primarily based on a evaluation of the literature, outcomes from a pilot research, or publicly accessible knowledge.
I’ve chosen to make use of the NHANES knowledge once more as a result of it contains the variables hypertension (highbp), age, and intercourse.
. webuse nhanes2
. logistic highbp c.age##ib1.intercourse
Logistic regression Variety of obs = 10,351
LR chi2(3) = 1675.19
Prob > chi2 = 0.0000
Log probability = -6213.1696 Pseudo R2 = 0.1188
------------------------------------------------------------------------------
highbp | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | 1.035184 .0018459 19.39 0.000 1.031572 1.038808
|
intercourse |
Feminine | .1556985 .0224504 -12.90 0.000 .1173677 .2065477
|
intercourse#c.age |
Feminine | 1.028811 .002794 10.46 0.000 1.02335 1.034302
|
_cons | .1690035 .0153794 -19.54 0.000 .1413957 .2020018
------------------------------------------------------------------------------
Word: _cons estimates baseline odds.
The output contains estimates of the percentages ratio for every of the variables in our mannequin. Odds ratios are exponentiated parameter estimates (that’s, (hat{{rm OR}_i} = e^{hat{beta_i}})), so we may specify the pure logarithms of the percentages ratios, (beta_i = {rm ln}({rm OR}_i)), as parameters in our energy simulations.
For instance, the estimate of the percentages ratio for age within the output above is 1.04, so we will specify (beta_1 = {rm ln}(hat{{rm OR}_{bf age}}) = {rm ln}(1.04) ).
We are able to additionally specify (beta_0 = {rm ln}(hat{{rm OR}_{bf cons}}) = {rm ln}(0.17) ), (beta_2 = {rm ln}(hat{{rm OR}_{bf intercourse}}) = {rm ln}(0.16) ), and (beta_3 = {rm ln}(hat{{rm OR}_{{bf age}instances {bf intercourse}}}) = {rm ln}(1.03) ).
Step 4: Simulate a dataset assuming the choice speculation, and match the mannequin
Subsequent, we create a simulated dataset primarily based on our assumptions concerning the mannequin below the choice speculation. The code block under is nearly equivalent to the code we used to create the info for our linear regression mannequin, however there are two essential variations. First, we use generate xb to create a linear mixture of the parameters and the simulated variables. The parameters are expressed because the pure logarithms of the percentages ratios estimated with the NHANES knowledge. Second, we use rlogistic(m,s) to create the binary dependent variable highbp from the variable xb.
clear set seed 123456 set obs 100 generate age = runiformint(18,65) generate feminine = rbinomial(1,0.5) generate work together = age*feminine generate xb = (ln(0.17) + ln(1.04)*age + ln(0.15)*feminine + ln(1.03)*work together) generate highbp = rlogistic(xb,1) > 0
We are able to then match a logistic regression mannequin to our simulated knowledge.
. logistic highbp age i.feminine c.age#i.feminine
Logistic regression Variety of obs = 100
LR chi2(3) = 14.95
Prob > chi2 = 0.0019
Log probability = -61.817323 Pseudo R2 = 0.1079
------------------------------------------------------------------------------
highbp | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | 1.055245 .0250921 2.26 0.024 1.007194 1.105589
1.feminine | .2365046 .3730999 -0.91 0.361 .0107404 5.207868
|
feminine#c.age |
1 | 1.015651 .0365417 0.43 0.666 .9464976 1.089857
|
_cons | .1578931 .151025 -1.93 0.054 .0242207 1.029293
------------------------------------------------------------------------------
Word: _cons estimates baseline odds.
Step 5: Write a program to create the datasets, match the fashions, and use simulate to check this system
Subsequent, let’s write a program that creates datasets below the choice speculation, matches logistic regression fashions, checks the null speculation, and makes use of simulate to run many iterations of this system.
The code block under incorporates the syntax for a program named simlogit. The default parameter values within the syntax command are the percentages ratios that we estimated utilizing the NHANES knowledge. And we use lrtest to check the null speculation that the percentages ratio for the age(instances )intercourse interplay equals 1.
seize program drop simlogit
program simlogit, rclass
model 16
// DEFINE THE INPUT PARAMETERS AND THEIR DEFAULT VALUES
syntax, n(integer) /// Pattern dimension
[ alpha(real 0.05) /// Alpha level
intercept(real 0.17) /// Intercept odds ratio
age(real 1.04) /// Age odds ratio
female(real 0.15) /// Female odds ratio
interact(real 1.03) ] // Interplay odds ratio
// GENERATE THE RANDOM DATA AND TEST THE NULL HYPOTHESIS
quietly {
drop _all
set obs `n'
generate age = runiformint(18,65)
generate feminine = rbinomial(1,0.5)
generate work together = age*feminine
generate xb = (ln(`intercept') + ln(`age')*age + ln(`feminine')*feminine + ln(`work together')*work together)
generate highbp = rlogistic(xb,1) > 0
logistic highbp age i.feminine c.age#i.feminine
estimates retailer full
logistic highbp age i.feminine
estimates retailer lowered
lrtest full lowered
}
// RETURN RESULTS
return scalar reject = (r(p)<`alpha')
finish
We then use simulate to run simlogit 100 instances utilizing the default parameter values.
. simulate reject=r(reject), reps(100): ///
> simlogit, n(500) intercept(0.17) age(1.04) feminine(.15) work together(1.03) alpha(0.05)
command: simlogit, n(500) intercept(0.17) age(1.04) feminine(.15)
> work together(1.03) alpha(0.05)
reject: r(reject)
Simulations (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
simulate saved the outcomes of the speculation checks to a variable named reject. The imply of reject is our estimate of the facility to detect an odds ratio of 1.03 for the age(instances )intercourse interplay time period assuming a pattern dimension of 500 individuals.
. summarize reject
Variable | Obs Imply Std. Dev. Min Max
-------------+---------------------------------------------------------
reject | 100 .53 .5016136 0 1
Step 6: Write a program known as power_cmd_simlogit
We may cease with our fast simulation if we had been solely in a particular set of assumptions. Nevertheless it’s straightforward to write down a further program known as power_cmd_simlogit which can enable us to make use of Stata’s energy command to create tables and graphs for a variety of pattern sizes.
seize program drop power_cmd_simlogit
program power_cmd_simlogit, rclass
model 16
// DEFINE THE INPUT PARAMETERS AND THEIR DEFAULT VALUES
syntax, n(integer) /// Pattern dimension
[ alpha(real 0.05) /// Alpha level
intercept(real 0.17) /// Intercept odds ratio
age(real 1.04) /// Age odds ratio
female(real 0.15) /// Female odds ratio
interact(real 1.03) /// Interaction odds ratio
reps(integer 100) ] // Variety of repetitions
// GENERATE THE RANDOM DATA AND TEST THE NULL HYPOTHESIS
quietly {
simulate reject=r(reject), reps(`reps'): ///
simlogit, n(`n') intercept(`intercept') age(`age') ///
feminine(`feminine') work together(`work together') alpha(`alpha')
summarize reject
native energy = r(imply)
}
// RETURN RESULTS
return scalar energy = r(imply)
return scalar N = `n'
return scalar alpha = `alpha'
return scalar intercept = `intercept'
return scalar age = `age'
return scalar feminine = `feminine'
return scalar work together = `work together'
finish
Step 7: Write a program known as power_cmd_simlogit_init
It’s additionally straightforward to write down a program known as power_cmd_simlogit_init which can enable us to simulate energy for a variety of values for the parameters in our mannequin.
seize program drop power_cmd_simlogit_init
program power_cmd_simlogit_init, sclass
sreturn native pss_colnames "intercept age feminine work together"
sreturn native pss_numopts "intercept age feminine work together"
finish
Utilizing energy simlogit
Now, we will use energy simlogit to simulate energy for quite a lot of assumptions. The instance under simulates energy for a variety of pattern sizes and impact sizes. Pattern sizes vary from 400 to 1000 individuals in increments of 200. And the percentages ratios for the age(instances )intercourse interplay time period vary from 1.02 to 1.05 in increments of 0.01.
. energy simlogit, n(400(200)1000) intercept(0.17) age(1.04) feminine(.15) work together(1.02(0.01)1.05) /// > reps(1000) desk graph(xdimension(work together) legend(rows(1))) Estimated energy Two-sided check +------------------------------------------------------------+ | alpha energy N intercept age feminine work together | |------------------------------------------------------------| | .05 .197 400 .17 1.04 .15 1.02 | | .05 .423 400 .17 1.04 .15 1.03 | | .05 .645 400 .17 1.04 .15 1.04 | | .05 .797 400 .17 1.04 .15 1.05 | | .05 .275 600 .17 1.04 .15 1.02 | | .05 .602 600 .17 1.04 .15 1.03 | | .05 .838 600 .17 1.04 .15 1.04 | | .05 .927 600 .17 1.04 .15 1.05 | | .05 .357 800 .17 1.04 .15 1.02 | | .05 .675 800 .17 1.04 .15 1.03 | | .05 .899 800 .17 1.04 .15 1.04 | | .05 .987 800 .17 1.04 .15 1.05 | | .05 .46 1,000 .17 1.04 .15 1.02 | | .05 .791 1,000 .17 1.04 .15 1.03 | | .05 .956 1,000 .17 1.04 .15 1.04 | | .05 .993 1,000 .17 1.04 .15 1.05 | +------------------------------------------------------------+
Determine 2: Estimated energy for the interplay time period in a logistic regression mannequin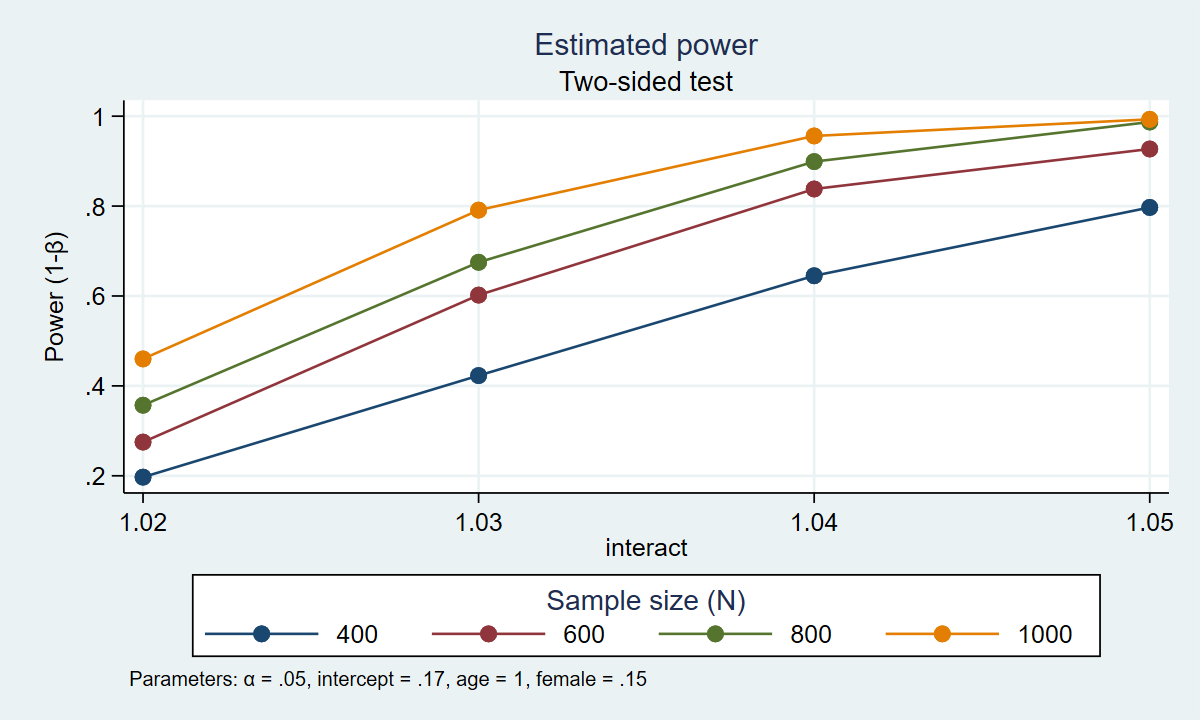
The desk and graph above point out that 80% energy is achieved with 4 combos of pattern dimension and impact dimension. Given our assumptions, we estimate that we are going to have no less than 80% energy to detect an odds ratio of 1.04 for pattern sizes of 600, 800, and 1000. And we estimate that we are going to have 80% energy to detect an odds ratio of 1.05 with a pattern dimension of 400 individuals.
On this weblog put up, I confirmed you learn how to simulate statistical energy for the interplay time period in each linear and logistic regression fashions. It’s possible you’ll be considering simulating energy for variations of those fashions, and you may modify the examples above to your personal functions. In my subsequent put up, I’ll present you learn how to simulate energy for multilevel and longitudinal fashions.

