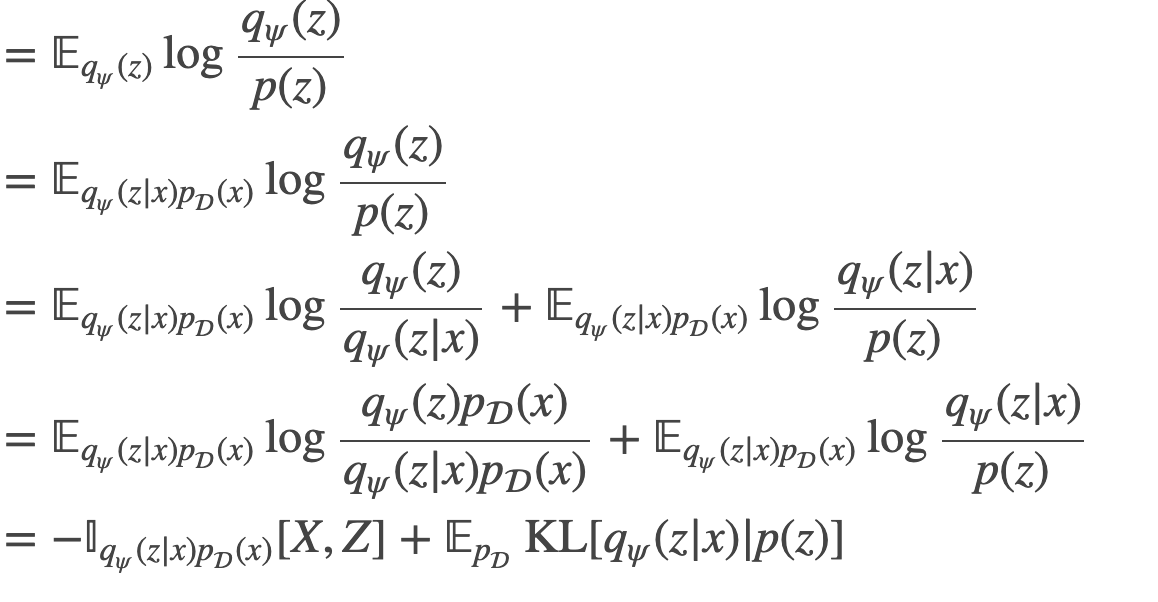visitor publish with Dóra Jámbor
This can be a half-guest-post written collectively with Dóra, a fellow participant in a studying group the place we just lately mentioned the unique paper on $beta$-VAEs:
On the floor of it, $beta$-VAEs are an easy extension of VAEs the place we’re allowed to immediately management the tradeoff between the reconstruction and KL loss phrases. In an try to raised perceive the place the $beta$-VAE goal comes from, and to additional encourage why it is smart, right here we derive $beta$-VAEs from totally different first rules than it’s offered within the paper. Over to largely Dóra for the remainder of this publish:
First, some notation:
- $p_mathcal{D}(mathbf{x})$: knowledge distribution
- $q_psi(mathbf{z}vert mathbf{x})$: illustration distribution
- $q_psi(mathbf{z}) = int p_mathcal{D}(mathbf{x})q_psi(mathbf{z}vert mathbf{x})$: combination posterior – marginal distribution of illustration $Z$
- $q_psi(mathbf{x}vert mathbf{z}) = frac{q_psi(mathbf{z}vert mathbf{x})p_mathcal{D}(mathbf{x})}{q_psi(mathbf{z})}$: “inverted posterior”
Motivation and assumptions of $beta$-VAEs
Studying disentangled representations that get better the unbiased knowledge generative elements has been a long-term aim for unsupervised illustration studying.
$beta$-VAEs had been launched in 2017 with a proposed modification to the unique VAE formulation that may obtain higher disentanglement within the posterior $q_psi(mathbf{z}vert mathbf{x})$. An assumption of $beta$-VAEs is that there are two units of latent elements, $mathbf{v}$ and $mathbf{w}$, that contribute to producing observations $x$ in the actual world. One set, $mathbf{v}$, is coordinate-wise conditionally unbiased given the noticed variable, i.e., $log p(mathbf{v}vert x) = sum_k log p(v_kvert mathbf{x})$. On the identical time, we do not assume something in regards to the remaining elements $mathbf{w}$.
The elements $v$ are going to be the primary object of curiosity for us. The conditional independence assumption permits us to formulate what it means to disentangle these elements of variation. Contemplate a illustration $mathbb{z}$ which entangles coordinates of $v$, in that every coordinate of $mathbb{z}$ relies on a number of coordinates of $mathbb{v}$, e.g. $z_1 = f_1(v_1, v_2)$ and $z_2 = f_2(v_1, v_2)$. Such a $mathbb{z}$ will not essentially fulfill co-ordinatewise conditional independence $log p(mathbf{z}vert x) = sum_k log p(z_kvert mathbf{x})$. Nevertheless, if every element of $mathbb{z}$ depended solely on one corresponding coordinate of $mathbf{v}$, for instance $z_1 = g_1(v_1)$ and $z_2 = g_2(v_2)$, the component-wise conditional independence would maintain for $mathbb{z}$ too.
Thus, underneath these assumptions we are able to encourage disentanglement to occur by encouraging the posterior $q_psi(mathbf{z}vert mathbf{x})$ to be coordinate-wise conditionally unbiased. This may be executed by including a brand new hyperparameter $beta$ to the unique VAE formulation
$$
mathcal{L}(theta, phi; x, z, beta) = -mathbb{E}_{q_{phi}(xvert z)p_mathcal{D}(x)}[log p_{theta}(x vert z)] + beta operatorname{KL} (q_{phi(zvert x)}| p(z)),
$$
the place $beta$ controls the trade-off between the capability of the latent info channel and studying conditionally unbiased latent elements. When $beta$ is greater than 1, we encourage the posterior $q_psi(zvert x)$ to be near the isotropic unit Gaussian $p(z) = mathcal{N}(0, I)$, which itself is coordnate-wise unbiased.
Marginal versus Conditional Independence
On this publish, we revisit the conditional independence assumption of latent elements, and argue {that a} extra applicable goal could be to have marginal independence within the latent elements. To point out you our instinct, let’s revisit the “Explaining Away” phenomenon from Probabilistic Graphical Fashions.
Explaining away
Contemplate three random variables:
$A$: Ferenc is grading exams
$B$: Ferenc is in a great temper
$C$: Ferenc is tweeting a meme
with the next graphical mannequin $A rightarrow C leftarrow B$.
Right here we might assume that Ferenc grading exams is unbiased of him being in a great temper, i.e., $A perp B$. Nevertheless, the stress of marking exams leads to elevated chance of procrastination, which will increase the probabilities of tweeting memes, too.
Nevertheless, as quickly as we see a meme being tweeted by him, we all know that he both in a great temper or he’s grading exams. If we all know he’s grading exams, that explains why he’s tweeting memes, so it is much less doubtless he is tweeting memes as a result of he is a great temper. Consequently, $A not!perp Bvert C$.
In all seriousness, if we have now a graphical mannequin $A rightarrow C leftarrow B$, in proof of $C$, independence between $A$ and $B$ not holds.
Why does this matter?
We argue that the explaining away phenomenon makes the conditional independence of latent elements undesirable. A way more cheap assumption in regards to the generative means of the info is that the elements of variation $mathbf{v}$ are drawn independently, after which the observations are generated conditoned on them. Nevertheless, if we contemplate two coordinates of $mathbb{v}$ and the remark $mathbf{x}$, we now have a $V_1 rightarrow mathbf{X} leftarrow V_2$ graphical mannequin, thus, conditional independence can’t maintain.
As an alternative, we argue that to get better the generative elements of the info, we should always encourage latent elements to be marginally unbiased. Within the subsequent part, we got down to derive an algorithm that encourages marginal independence within the illustration Z. We may even present how the ensuing loss operate from this new derivation is definitely equal to the unique $beta$-VAEs formulation.
Marginally Unbiased Latent Components
We’ll begin from desired properties of the illustration distribution $q_psi(zvert x)$. We might like this illustration to fulfill two properties:
- Marginal independence: We wish the mixture posterior $q_psi(z)$ to be near some fastened and factorized unit Gaussian prior $p(z) = prod_i p(z_i)$. This encourages $q_psi(z)$ to exhibit coordinate-wise independence.
- Most Info: We might just like the illustration $Z$ to retain as a lot info as attainable in regards to the enter knowledge $X$.
Notice that with out (1), (2) is inadequate, as a result of then any deterministic and invertible operate of $X$ would include most details about $X$ however that would not make it a helpful or disentangled illustration. Equally, with out (2), (1) is inadequate as a result of if we set $q_psi(zvert x) = p(z)$ it could give us a latent illustration Z that’s coordinate-wise unbiased, however additionally it is unbiased of the info which isn’t very helpful.
Deriving a sensible goal
We are able to obtain a mix of those desiderata by optimizing an goal with the weighted mixture of two phrases comparable to the 2 objectives we set out above:
$$
mathcal{L}(psi) = operatorname{KL}[q_psi(z)| p(z)] – lambda mathbb{I}_{q_psi(zvert x) p_mathcal{D}(x)}[X, Z]
$$
Bear in mind, we use $q_psi(z)$ to indicate the mixture posterior. We are going to seek advice from this because the InfoMax goal. Now we will present how this goal could be associated to the $beta$-VAE goal. Let’s first contemplate the KL time period within the above goal:
start{align}
operatorname{KL}[q_psi(z)| p(z)] &= mathbb{E}_{q_psi(z)} log frac{q_psi(z)}{p(z)}
&= mathbb{E}_{q_psi(zvert x)p_mathcal{D}(x)} log frac{q_psi(z)}{p(z)}
&= mathbb{E}_{q_psi(zvert x)p_mathcal{D}(x)} log frac{q_psi(z)}{q_psi(zvert x)} + mathbb{E}_{q_psi(zvert x)p_mathcal{D}(x)} log frac{q_psi(zvert x)}{p(z)}
&= mathbb{E}_{q_psi(zvert x)p_mathcal{D}(x)} log frac{q_psi(z)p_mathcal{D}(x)}{q_psi(zvert x)p_mathcal{D}(x)} + mathbb{E}_{q_psi(zvert x)p_mathcal{D}(x)} log frac{q_psi(zvert x)}{p(z)}
&= -mathbb{I}_{q_psi(zvert x)p_mathcal{D}(x)}[X,Z] + mathbb{E}_{p_mathcal{D}}operatorname{KL}[q_psi(zvert x)| p(z)]
finish{align}
That is attention-grabbing. If the mutual info between $X$ and $Z$ is non-zero (which is ideally the case), the above equation reveals that latent elements can’t be each marginally and conditionally unbiased on the identical time. It additionally offers us a solution to relate the KL phrases representing marginal and conditional independence.
Placing this again into the InfoMax goal, we have now that
start{align}
mathcal{L}(psi) &= operatorname{KL}[q_psi(z)| p(z)] – lambda mathbb{I}_{q_psi(zvert x)p_mathcal{D}(x)}[X, Z]
&= mathbb{E}_{p_mathcal{D}}operatorname{KL}[q_psi(zvert x)| p(z)] – (lambda + 1) mathbb{I}_{q_psi(zvert x)p_mathcal{D}(x)}[X, Z]
finish{align}
Utilizing the KL time period within the InfoMax goal, we had been in a position to get better the KL-divergence time period that additionally seems within the $beta$-VAE (and consequently, VAE) goal.
At this level, we nonetheless have not outlined the generative mannequin $p_theta(xvert z)$, the above goal expresses all the pieces when it comes to the info distribution $p_mathcal{D}$ and the posterior/illustration distribution $q_psi$.
We are going to now concentrate on the 2nd time period in our desired goal, the weighted mutual info, which we nonetheless cannot simply consider. We are going to now present that we are able to get better the reconstruction time period in $beta$-VAEs by doing a variational approximation to the mutual info.
Variational certain on mutual info
Notice the next equality:
start{equation}
mathbb{I}[X,Z] = mathbb{H}[X] – mathbb{H}[Xvert Z]
finish{equation}
Since we pattern X from the info distribution $p_mathcal{D}$, we see that the primary time period $mathbb{H}[X]$, the entropy of $X$, is fixed with respect to the variational parameter $psi$. We’re left to concentrate on discovering a great approximation to the second time period $mathbb{H}[Xvert Z]$. We are able to accomplish that by minimizing the KL divergence between $q_psi(xvert z)$ and an auxilliary distribution $p_theta(xvert z)$ to make a variational appoximation to the mutual info:
$$mathbb{H}[Xvert Z] = – mathbb{E}_{qpsi(zvert x)p_mathcal{D}(x)} log q_psi(xvert z) leq inf_theta – mathbb{E}_{qpsi(zvert x)p_mathcal{D}(x)} log p_theta(xvert z)$$
Placing this certain again collectively:
Discovering this decrease certain to MI, we have now now recovered the reconstruction time period from the $beta$-VAE goal:
$$
mathcal{L}(psi) + textual content{const} leq – (1 + lambda) mathbb{E}_{q_psi(zvert x)p_mathcal{D}(x)} log p_theta(xvert z) + mathbb{E}_{p_mathcal{D}}operatorname{KL}[q_psi(zvert x)| p(z)]
$$
That is primarily the identical because the $beta$-VAE goal operate, the place $beta$ is said to our earlier $lambda$. Specifically, $beta = frac{1}{1 + lambda}$. Thus, since we assumed $lambda>0$ for the InfoMax goal to make sense, we are able to say that the $beta$-VAE goal encourages disentanglement within the InfoMax sense for values of $0<beta<1$.
Takeaways
Conceptually, this derivation is attention-grabbing as a result of the primary object of curiosity is now the popularity mannequin, $q_psi(zvert x)$. That’s, the posterior turns into a the main focus of the target operate – one thing that’s not the case once we are maximizing mannequin chance alone (as defined right here). On this respect, this derivation of the $beta$-VAE makes extra sense from a illustration studying viewpoint than the derivation of VAE from most chance.
There’s a good symmetry to those two views. There are two joint distributions over latents and observable variables in a VAE. On one hand we have now $q_psi(zvert x)p_mathcal{D}(x)$ and on the opposite we have now $p(x)p_theta(xvert z)$. The “latent variable mannequin” $q_psi(zvert x)p_mathcal{D}(x)$ is a household of LVMs which has a marginal distribution on observable $mathbf{x}$ that’s precisely the identical as the info distribution $p_mathcal{D}$. So one can say $q_psi(zvert x)p_mathcal{D}(x)$ is a parametric household of latent variable fashions with whose chances are maximal – and we need to select from this household a mannequin the place the illustration $q_psi(zvert x)$ has good properties.
On the flipside, $p(z)p_theta(xvert z)$ is a parametic set of fashions the place the marginal distribution of latents is coordinatewise unbiased, however we wish to select from this household a mannequin that has good knowledge chance.
The VAE goal tries to maneuver these two latent variable fashions nearer to 1 one other. From the angle of $q_psi(zvert x)p_mathcal{D}(x)$ this quantities to reproducing the prior $p(z)$ with the mixture posterior. from the angle of $p(z)p_theta(xvert z)$, it quantities to maximising the info chance. When the $beta$-VAE goal is used, we moreover want to maximise the mutual info between the noticed knowledge and the illustration.
This twin function of data maximization and most chance has been identified earlier than, for instance on this paper in regards to the IM algorithm. The symmetry of variational studying has been exploited just a few instances, for instance in yin-yang machines, and extra just lately additionally in strategies like adversarially realized inference.