Spherical geometry
In spherical geometry, the inside angles of a triangle add as much as greater than π. And in reality you may decide the realm of a spherical triangle by how a lot the angle sum exceeds π. On a sphere of radius 1, the realm equals the triangle extra
Space = E = inside angle sum − π.
Small triangles have inside angle sum close to π. However you can, for instance, have a triangle with three proper angles: put a vertex on the north pole and two vertices on the equator 90° longitude aside.
Hyperbolic geometry
In hyperbolic geometry, the sum of the inside angles of a triangle is all the time lower than π. In an area with curvature −1, the realm equals the triangle defect, the distinction between π and the angle sum.
Space = D = π − inside angle sum.
Once more small triangles have an inside angle sum close to π. Each spherical and hyperbolic geometry are regionally Euclidean.
The inside angle sum will be any worth lower than π, and in order the angle sum goes to 0, the triangle defect, and therefore the realm, goes to π. Because the minimal angle sum is 0, the utmost space of a triangle is π.
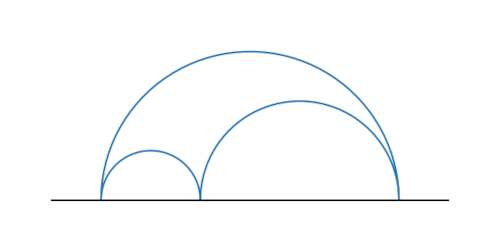
The determine under has inside angle sum 0 and space π in hyperbolic geometry.
Strictly talking that is an improper triangle as a result of the three hyperbolic traces (i.e. half circles) don’t intersect throughout the hyperbolic aircraft per se however at splendid factors on the true axis. However you can come as near this triangle as you want, staying throughout the hyperbolic aircraft.
Notice that the radii of the (Euclidean) half circles doesn’t change the realm. Any three semicircles that intersect on the true line as above make a triangle with the identical space. Notice additionally that the triangle has infinite perimeter however finite space.