Bowie’s ODE solver and the nonlinear pendulum

I not too long ago realized of Bowie’s numerical methodology for fixing abnormal differential equations of the shape

y″ = f(y)

by way of Alex Scarazzini’s masters thesis [1].

The one reference I’ve been capable of finding for the strategy, apart from [1], is the NASA Orbital Flight Handbook from 1963. The handbook describes the strategy as “a way employed by C. Bowie and integrated in lots of Martin applications” and says nothing extra about its origin.

Martin Firm

What does it imply by “Martin applications”? The primary line of the foreword of the handbook says

This handbook has been produced by the House Programs Division of the Martin Firm underneath Contract NAS8-S03l with the George C. Marshall House Flight Middle of the Nationwide Aeronautics and House Administration.

The Martin Firm was the Glenn L. Martin Firm, which turned Martin Marietta after merging with American-Marietta Company in 1961. The handbook was written after the merger however used the older title. Martin Marietta would go on to develop into Lockheed Martin in 1995.

Bowie’s methodology was used “in lots of Martin applications” and but is virtually unknown in educational circles. Scarazzini’s thesis reveals the strategy works nicely for his downside.

Nonlinear pendulum

My first thought once I noticed the type of differential equations Bowie’s methodology solves was the nonlinear pendulum equation

y″ = − sin(y)

the place the preliminary displacement y(0) is just too massive for the approximation sin θ ≈ θ to be sufficiently correct. I wrote some Python code to check out Bowie’s methodology on this equation.

import numpy as np

N = 100
y  = np.zeros(N)
yp = np.zeros(N) # y'

y[0] = 1
yp[0] = 0

T = 4*ellipk(np.sin(y[0]/2)**2)
h = T/N

f   = lambda x: -np.sin(x)
fp  = lambda x: -np.cos(x) # f'
fpp = lambda x:  np.sin(x) # f''

for n in vary(0, N-1):
    y[n+1] = y[n] + h*yp[n] + 0.5*h**2*f(y[n]) + 
              (h**3/6)*fp(y[n])*yp[n] + 
              (h**4/24)*(fpp(yp[n])**2 + fp(y[n])*f(y[n]))
    yp[n+1] = yp[n] + h*f(y[n]) + 0.5*h**2*fp(y[n])*yp[n] + 
              (h**3/6)*(fpp(yp[n])**2 + fp(y[n])*f(y[n]))

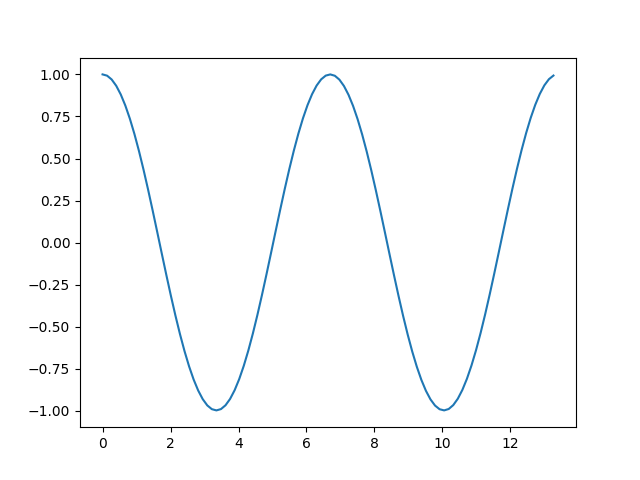
Right here’s a graph of the numerical resolution.

The answer appears like a cosine, but it surely isn’t precisely. As I clarify right here,

The answer to the nonlinear pendulum equation can also be periodic, although the answer is a mix of Jacobi features slightly than a mix of trig features. The distinction between the 2 options is small when θ₀ is small, however turns into extra vital as θ₀ will increase.

The distinction within the intervals is extra evident than the distinction in form for the 2 waves. The interval of the nonlinear resolution is longer than that of the linearized resolution.

That’s why the interval T within the code is just not

2π = 6.28

however slightly

4 Ok(sin² θ₀/2) = 6.70.

You’ll additionally see the interval of the nonlinear pendulum given as 4 Ok(sin θ₀/2). As identified within the article linked above,

There are two conventions for outlining the whole elliptic integral of the primary sort. SciPy makes use of a conference for Ok that requires us to sq. the argument.

Associated posts

[1] Alex Scarazzini.3D Visualization of a Schwarzschild Black Gap Atmosphere. College of Bern. August 2025.