Machine studying, deep studying, and synthetic intelligence are a set of algorithms used to establish patterns in information. These algorithms have exotic-sounding names like “random forests”, “neural networks”, and “spectral clustering”. On this submit, I’ll present you how one can use one in every of these algorithms known as a “assist vector machines” (SVM). I don’t have area to elucidate an SVM intimately, however I’ll present some references for additional studying on the finish. I’m going to provide you a quick introduction and present you how one can implement an SVM with Python.
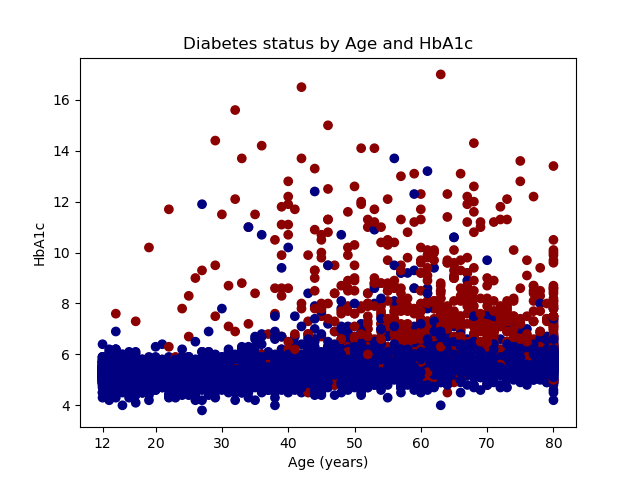
Our aim is to make use of an SVM to distinguish between people who find themselves more likely to have diabetes and those that should not. We’ll use age and HbA1c stage to distinguish between folks with and with out diabetes. Age is measured in years, and HbA1c is a blood check that measures glucose management. The graph under shows diabetics with pink dots and nondiabetics with blue dots. An SVM mannequin predicts that older folks with larger ranges of HbA1c within the red-shaded space of the graph usually tend to have diabetes. Youthful folks with decrease HbA1c ranges within the blue-shaded space are much less more likely to have diabetes.
In case you are not aware of Python, it could be useful to learn the primary 4 posts in my Stata/Python integration sequence earlier than you learn additional.
- Organising Stata to make use of Python
- 3 ways to make use of Python in Stata
- The right way to set up Python packages
- The right way to use Python packages
Obtain, merge, and clear the info
We can be utilizing information from america Nationwide Well being and Diet Examination Survey (NHANES). Particularly, we can be utilizing the variables age from the demographic information,
HbA1c from the glycohemoglobin information, and diabetes from the diabetes information.
The code block under imports three SAS Transport recordsdata from the NHANES web site,
saves the recordsdata to Stata datasets, merges the Stata datasets, renames and recodes the variables, holds the variables diabetes, age, and HbA1c, drops observations with lacking values, and saves the variables to a dataset named diabetes.dta. The final two traces of the code block erase the short-term datasets age.dta and glucose.dta.
import sasxport5 "https://wwwn.cdc.gov/Nchs/Nhanes/2015-2016/DEMO_I.XPT", clear save age.dta, change import sasxport5 "https://wwwn.cdc.gov/Nchs/Nhanes/2015-2016/GHB_I.XPT", clear save glucose.dta, change import sasxport5 "https://wwwn.cdc.gov/Nchs/Nhanes/2015-2016/DIQ_I.XPT", clear save diabetes, change merge 1:1 seqn utilizing "glucose.dta" drop _merge merge 1:1 seqn utilizing "age.dta" rename ridageyr age rename lbxgh HbA1c rename diq010 diabetes recode diabetes (1 = 1) (2/3 = 0) (9=.) hold diabetes age HbA1c drop if lacking(diabetes, age, HbA1c) save diabetes, change erase age.dta erase glucose.dta
Let’s listing the primary 5 observations within the dataset to test our work.
. listing in 1/5
+------------------------+
| diabetes HbA1c age |
|------------------------|
1. | 1 7 62 |
2. | 0 5.5 53 |
3. | 1 5.8 78 |
4. | 0 5.6 56 |
5. | 0 5.6 42 |
+------------------------+
We are able to additionally tabulate diabetes to confirm that it has two classes, the place 1 signifies the presence of diabetes and 0 signifies the absence of diabetes.
. tabulate diabetes
Physician instructed |
you will have |
diabetes | Freq. % Cum.
------------+-----------------------------------
0 | 5,531 87.49 87.49
1 | 791 12.51 100.00
------------+-----------------------------------
Whole | 6,322 100.00
Open and graph the uncooked information utilizing Python
Subsequent, let’s learn the Stata dataset diabetes.dta right into a pandas information body named information and plot the uncooked information. I’ve included feedback within the code block under to briefly clarify every part. We start the code block by importing the pandas module utilizing the alias pd, the pyplot module from the matplotlib package deal utilizing the alias plt, and the colours module from the matplotlib package deal utilizing the alias mcolors.
Then, we are able to use the pandas technique read_stata() to learn the Stata dataset diabetes right into a pandas information body named information. The choice convert_categoricals=False tells pandas to learn labeled numeric information, resembling diabetes, as numbers quite than changing the numbers to their categorical labels. The choice preserve_dtypes=True instructs pandas to learn the Stata variables with out changing their storage sort. For instance, Stata integers can be transformed to integers within the pandas information body. The choice convert_missing=False tells pandas to learn lacking values within the Stata dataset to lacking values within the pandas information body.
The subsequent two Python statements place the variables age and HbA1c right into a pandas information body named X and the variable diabetes right into a pandas sequence named y. In statistical jargon, we might confer with the variables in X because the “unbiased variables” and the variable in y because the “dependent variable”. In machine-learning jargon, we might confer with the variables in X because the “characteristic variables” and y because the “goal variable”. The aim is to make use of the knowledge in X to tell apart between classes of y.
We are able to plot the uncooked information utilizing the scatter() technique within the pyplot module. The primary argument specifies that age can be plotted on the horizontal axis. The second argument specifies that HbA1c can be plotted on the vertical axis. The third argument, c=y, specifies that completely different colours are for use for various values of y. And the fourth argument makes use of the ListedColormap() technique within the colours module to specify the show colours for classes of y. Recall that y is an indicator for diabetes, so observations the place y=0 can be displayed with a navy marker and observations the place y=1 can be displayed with a dark-red marker.
The remaining statements that start with plt label the axes, outline the axis ticks, create a title for the graph, and save the graph to a file named scatterplot.png.
python: # Import the required packages import pandas as pd import matplotlib.pyplot as plt import matplotlib.colours as mcolors # Learn the Stata dataset into Python information = pd.read_stata('diabetes.dta', convert_categoricals=False, preserve_dtypes=True, convert_missing=False) # Outline the characteristic matrix (unbiased variables) # and the goal variable (dependent variable) X = information[['age','HbA1c']] y = information['diabetes'] # Plot the uncooked information plt.scatter(X['age'], X['HbA1c'], c=y, cmap = mcolors.ListedColormap(["navy", "darkred"])) plt.xlabel('Age (years)') plt.ylabel('HbA1c') plt.xticks((12,20,30,40,50,60,70,80)) plt.yticks((4,6,8,10,12,14,16)) plt.title('Diabetes standing by Age and HbA1c') # Save the graph plt.savefig("scatterplot.png")
Our graph reveals that individuals with diabetes are typically older and have larger ranges of HbA1c.
Break up the info into coaching and testing datasets
It’s common observe in machine studying to separate the info right into a coaching dataset and a testing dataset. The coaching information are used to develop a mannequin, and the testing dataset is used to test for consistency. This helps us keep away from fashions which can be overfit to a selected dataset and don’t generalize to different datasets.
We’ll start the code block under by importing the train_test_split() technique from the model_selection module within the sklearn package deal.
Subsequent, we’ll use the train_test_split() technique to separate the info. The characteristic object X is cut up right into a coaching characteristic object named X_train and a testing characteristic object named X_test. The goal object y is cut up right into a coaching goal object named y_train and a testing goal object named y_test. The choice test_size=0.4 specifies that 40% of the info are put aside for testing the mannequin and 60% of the info put aside for coaching the mannequin. The cut up is a random course of, and the choice random_state=0 units the random-number seed in order that our outcomes are reproducible.
python: from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0) finish
Selecting the parameters for our SVM mannequin utilizing a grid search and cross-validation
There are completely different sorts of SVMs, and we can be becoming a c-support vector classifier (SVC) utilizing the SVC() technique within the svm module of the sklearn package deal. We’ll specify three arguments for our SVC mannequin: the kernel operate, the diploma of the kernel operate, and the regularization parameter (C). The syntax will look much like the assertion under.
svm.SVC(kernel, diploma, regularization parameter (C))
Let’s specify a polynomial kernel operate and use the coaching dataset to pick out the diploma and regularization parameters. We are able to specify a listing of believable values for each parameters, practice the mannequin utilizing all attainable mixtures of each parameters, and choose the mix that produces the best-fitting mannequin.
Let’s additionally use a method known as “k-fold cross-validation” for our grid search. Cross-validation begins by splitting our coaching dataset into okay subgroups. We’ll practice the SVC mannequin on the k-1 subgroups and check the mannequin on the kth subgroup. We’ll repeat this course of okay instances so that every of the subgroups serves as a testing group. Then, we’ll calculate the typical of the outcomes.
We start the code block under by importing modules and strategies from the sklearn package deal. We’ll import the svm module from the sklearn package deal. And we’ll import the cross_val_score and GridSearchCV strategies from the model_selection module within the sklearn package deal.
The subsequent part of our code block performs the grid search utilizing k-fold cross-validation. We start by defining an object named mannequin that specifies a polynomial kernel operate for the SVC mannequin. Subsequent, we outline a dictionary object named parameters that shops believable parameter values for diploma and C. Subsequent, we outline an object named poly_svc that accommodates the outcomes of our grid search. We’ll specify 4 arguments for the GridSearchCV() technique. The primary argument is the mannequin, the second argument is the listing of parameters, and the third argument is the variety of folds (okay) for cross-validation. We’ve specified 10-fold cross-validation. The fourth argument specifies that accuracy is used to evaluate the match (rating) of the mannequin. The choice .match(X_train, y_train) tells GridSearchCV to coach the mannequin utilizing the coaching dataset.
The match() technique assesses the match of our SVM mannequin, and we are able to print the outcomes saved in best_params_.
python: from sklearn import svm from sklearn.model_selection import cross_val_score from sklearn.model_selection import GridSearchCV # Do a grid seek for the parameters "diploma" and "C" utilizing 10-fold # cross-validation mannequin = svm.SVC(kernel="poly") parameters = {'diploma':[1,2,3], 'C':[1,2,3]} poly_svc = GridSearchCV(mannequin, parameters, cv=10, scoring='accuracy').match(X_train, y_train) # Show the parameters that yield the best-fitting mannequin poly_svc.match(X_train,y_train) print(poly_svc.best_params_) finish
Let’s view the output from the code block above. The outcomes of the grid search inform us that the mannequin matches greatest when C equals 3 and diploma equals 3.
>>> poly_svc.match(X_train,y_train)
GridSearchCV(cv=10, estimator=SVC(kernel="poly"),
param_grid={'C': [1, 2, 3], 'diploma': [1, 2, 3]},
scoring='accuracy')
>>> print(poly_svc.best_params_)
{'C': 3, 'diploma': 3}
Check the mannequin on the testing dataset
Now we’re prepared to check the match of our mannequin utilizing the testing dataset. The primary line of the code block under makes use of the coaching dataset to suit an SVM mannequin with the parmeters C equals 3 and diploma equals 3.
The second line of the code block under makes use of the cross_val_score() technique of the model-selection module within the sklearn package deal to estimate the accuracy of the mannequin. The primary argument specifies the poly_svc mannequin that we match utilizing the coaching dataset. The second and third arguments specify the testing information X_test and y_test. The fourth argument specifies 10-fold cross-validation. And the fifth argument specifies that we’ll use prediction accuracy because the rating to guage the mannequin.
The third line of the code block under shows the estimated accuracy of our SVM mannequin utilizing the testing dataset. The accuracy for every cross-validation is saved within the object scores. The print() technique shows the imply and two customary deviations of accuracy.
# Match the SVM mannequin utilizing the parameters chosen from the grid search
poly_svc = svm.SVC(kernel="poly", diploma=3, C=3).match(X_train, y_train)
scores = cross_val_score(poly_svc, X_test, y_test, cv=10, scoring='accuracy')
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.imply(), scores.std() * 2))
The output under tells us that our SVM mannequin predicts diabetes standing with 93% accuracy (+/- 0.03).
poly_svc = svm.SVC(kernel="poly", diploma=3, C=3).match(X_train, y_train)
scores = cross_val_score(poly_svc, X_test, y_test, cv=10, scoring='accuracy')
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.imply(), scores.std() * 2))
Accuracy: 0.93 (+/- 0.03)
Plot the outcomes of the SVM mannequin
Let’s graph the outcomes of our SVM mannequin utilizing a contour plot. The primary set of statements within the code block under makes use of the meshgrid() technique within the NumPy package deal to create a two-dimensional grid. The x dimension ranges from the minimal worth of age to the utmost worth of age. The y dimension ranges from the minimal worth of HbA1c to the utmost worth of HbA1c. The step measurement, or increment, of the grid is specified with h=0.1.
The second set of statements within the code block under makes use of the predict() technique within the svm module of the sklearn package deal to categorise every level within the grid as “diabetic” or “not diabetic”. Then, we use the contourf() technique within the pyplot module of the matplotlib package deal to create a contour plot of the grid. The ListedColormap() technique within the colours module of the matplotlib package deal specifies that “nondiabetic” areas of the graph can be shaded with the colour “dodgerblue” and “diabetic” areas of the graph can be shaded with the colour “pink”.
# Create a mesh on which to plot the outcomes of the SVM mannequin h = 0.1 # step measurement within the mesh x_min, x_max = X['age'].min() - 1, X['age'].max() + 1 y_min, y_max = X['HbA1c'].min() - 1, X['HbA1c'].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # Plot the anticipated determination boundary Z = poly_svc.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.form) plt.contourf(xx, yy, Z, cmap = mcolors.ListedColormap(["dodgerblue", "red"]), alpha=0.8)
And eventually, we are able to overlay a scatterplot of the uncooked information on the contour plot and save the graph. This is similar scatterplot that we created earlier.
# Plot the uncooked information on the anticipated determination boundary plt.scatter(X['age'], X['HbA1c'], c=y, cmap = mcolors.ListedColormap(["navy", "darkred"])) plt.xlabel('Age (years)') plt.ylabel('HbA1c') plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.xticks((12,20,30,40,50,60,70,80)) plt.yticks((4,6,8,10,12,14,16)) plt.title('Diabetes standing by Age and HbA1c') # Save the graph plt.savefig("contourplot.png")
Conclusion
We did it! We used an SVM algorithm to categorise folks as diabetic or nondiabetic primarily based on their age and HbA1c values. Our mannequin appropriately classifies 93% of the folks in our testing dataset. You possibly can use the same technique to differentiate between folks or observations in different classes. For instance, Josh Starmer’s YouTube video Help Vector Machines in Python from Begin to End demonstrates how one can use SVMs to categorise folks as being more likely to default on loans or not. We’ve barely scratched the floor of the machine-learning capabilities of the Scikit-learn package deal, and yow will discover many examples on their web site. And the most effective half is that you would be able to simply make this a part of your full evaluation that entails information cleansing, exploration, and different mannequin becoming in Stata.
I’ve included hyperlinks to some books, papers, Github repositories, and YouTube movies under. And I’ve gathered all of the code from this weblog submit under and added feedback to remind you of the aim of the code.
I hope that this submit and my earlier posts about Three-dimensional floor plots of marginal predictions and Working with APIs and JSON information have given you some concepts for issues that you just would possibly love to do with Python and Stata. In my subsequent submit, I’ll introduce the Stata Perform Interface (SFI), which lets you transfer particular person variables, matrices, scalars, macros, and different info backwards and forwards between Stata and Python.
Additional studying and viewing
Cristianini, N., and J. Shawe-Taylor. 2000. An Introduction to Help Vector Machines and Different Kernel-based Studying Strategies. Cambridge: Cambridge College Press.
Droste, M. 2020. Stata pylearn.
Guenther, N., and M. Schonlau. 2016. Help vector machines. Stata Journal 16: 917–937.
Hastie, T., R. Tibshirani, and J. Friedman. 2016. The Parts of Statistical Studying: Information Mining, Inference, and Prediction, 2nd ed. New York: Springer-Verlag.
Starmer, J. 2018. Video: Machine Studying Fundamentals: Cross Validation.
——. 2019. Video: Help Vector Machines, Clearly Defined!!!.
——. 2019. Video: Help Vector Machines Half 2: The Polynomial Kernel.
——. 2019. Video: Help Vector Machines Half 3: The Radial (RBF) Kernel.
——. 2020. Video: Help Vector Machines in Python from Begin to End.
instance.do
// Import the info from the CDC web site import sasxport5 "https://wwwn.cdc.gov/Nchs/Nhanes/2015-2016/DEMO_I.XPT", clear save age.dta, change import sasxport5 "https://wwwn.cdc.gov/Nchs/Nhanes/2015-2016/GHB_I.XPT", clear save glucose.dta, change import sasxport5 "https://wwwn.cdc.gov/Nchs/Nhanes/2015-2016/DIQ_I.XPT", clear save diabetes, change // Merge the three recordsdata merge 1:1 seqn utilizing "glucose.dta" drop _merge merge 1:1 seqn utilizing "age.dta" // Rename and recode the variables rename ridageyr age rename lbxgh HbA1c rename diq010 diabetes recode diabetes (1 = 1) (2/3 = 0) (9=.) // Preserve the variables of curiosity, drop lacking values, and save the dataset hold diabetes age HbA1c drop if lacking(diabetes, age, HbA1c) save diabetes, change // Erase the short-term NHANES datasets erase age.dta erase glucose.dta python: # Import Python packages import numpy as np import pandas as pd import matplotlib.pyplot as plt import matplotlib.colours as mcolors from sklearn import svm, datasets from sklearn.svm import SVC from sklearn.model_selection import train_test_split from sklearn.model_selection import cross_val_score from sklearn.model_selection import GridSearchCV # Learn the Stata dataset into Python information = pd.read_stata('diabetes.dta', convert_categoricals=False, preserve_dtypes=True, convert_missing=False) # Outline the characteristic matrix (unbiased variables) # and the goal variable (dependent variable) X = information[['age','HbA1c']] y = information['diabetes'] # Plot the uncooked information plt.scatter(X['age'], X['HbA1c'], c=y, cmap = mcolors.ListedColormap(["navy", "darkred"])) plt.xlabel('Age (years)') plt.ylabel('HbA1c') plt.xticks((12,20,30,40,50,60,70,80)) plt.yticks((4,6,8,10,12,14,16)) plt.title('Diabetes standing by Age and HbA1c') # Save the graph plt.savefig("scatterplot.png") # Break up the info into coaching (60%) and testing (40%) information X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0) # Do a grid seek for the parameters "diploma" and "C" utilizing 10-fold # cross-validation mannequin = svm.SVC(kernel="poly") parameters = {'diploma':[1,2,3], 'C':[1,2,3]} poly_svc = GridSearchCV(mannequin, parameters, cv=10, scoring='accuracy').match(X_train, y_train) # Show the parameters that yield the best-fitting mannequin poly_svc.match(X_train,y_train) print(poly_svc.best_params_) # Match the SVM mannequin utilizing the parameters chosen from the grid search poly_svc = svm.SVC(kernel="poly", diploma=3, C=3).match(X_train, y_train) scores = cross_val_score(poly_svc, X_test, y_test, cv=10, scoring='accuracy') print("Accuracy: %0.2f (+/- %0.2f)" % (scores.imply(), scores.std() * 2)) # Create a mesh on which to plot the outcomes of the SVM mannequin h = 0.1 # step measurement within the mesh x_min, x_max = X['age'].min() - 1, X['age'].max() + 1 y_min, y_max = X['HbA1c'].min() - 1, X['HbA1c'].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # Plot the anticipated determination boundary Z = poly_svc.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.form) plt.contourf(xx, yy, Z, cmap = mcolors.ListedColormap(["dodgerblue", "red"]), alpha=0.8) # Plot the uncooked information on the anticipated determination boundary plt.scatter(X['age'], X['HbA1c'], c=y, cmap = mcolors.ListedColormap(["navy", "darkred"])) plt.xlabel('Age (years)') plt.ylabel('HbA1c') plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.xticks((12,20,30,40,50,60,70,80)) plt.yticks((4,6,8,10,12,14,16)) plt.title('Diabetes standing by Age and HbA1c') # Save the graph plt.savefig("contourplot.png") finish