Why you shouldn’t use imply imputation for lacking knowledge

I encountered the query in the present day of what to do with lacking values when conducting null speculation testing or regression? I’ve seen many counsel doing imply imputation. That’s, merely exchange any lacking values with the imply of the variable calculated from the noticed values. I argue that imply imputation is worse than doing nothing. Let’s discover.

To start, let’s simulate a vector, x, from the random regular distribution.

set.seed(2112)
x <- rnorm(100, imply = 0, sd = 1)
(mean1 <- imply(x))

(sd1 <- sd(x))

We are able to see that the imply and normal deviation aver pretty near 0 and 1, respectively. Within the subsequent code chunk we’re going to randomly choose 20% of observations and set the worth to NA. We are able to calculate the imply and normal deviation excluding the lacking values (i.e. NAs) however setting na.rm = TRUE. The imply and normal deviation are comparatively shut.

x[sample(length(x), length(x) * 0.2, replace = FALSE)] <- NA
(mean2 <- imply(x, na.rm = TRUE))

(sd2 <- sd(x, na.rm = TRUE))

Now we are going to exchange the NAs we launched above with the imply. We are able to see that the usual deviation is sort of a bit smaller, therefore lowering the variance of our estimate. Since lots of our statistical exams depend on variance, lowering the variance could result in spurious conclusions.

x[is.na(x)] <- imply(x, na.rm = TRUE)
(mean3 <- imply(x))

(sd3 <- sd(x))

To point out this isn’t a random anomaly for our one random pattern, let’s repeat the above 1,000 occasions.

n_samples <- 1000
percent_missing <- 0.10
sd_diffs <- knowledge.body(pattern = 1:n_samples,
                       sd_drop_miss = numeric(n_samples),
                       sd_impute_miss = numeric(n_samples))
for(i in seq_len(n_samples)) {
    x2 <- x
    x2[sample(length(x), length(x) * percent_missing, replace = FALSE)] <- NA
    sd_diffs[i,]$sd_drop_miss <- sd(x2, na.rm = TRUE)
    x2[is.na(x2)] <- imply(x2, na.rm = TRUE)
    sd_diffs[i,]$sd_impute_miss <- sd(x2)
}

sd_diffs |> 
    reshape2::soften(id.vars="pattern", variable.title="calculation_type", worth.title="sd") |>
    ggplot(aes(x = sd, coloration = calculation_type)) +
        geom_vline(xintercept = sd(x)) +
        geom_density() +
        xlab('Customary Deviation') +
        theme_minimal()

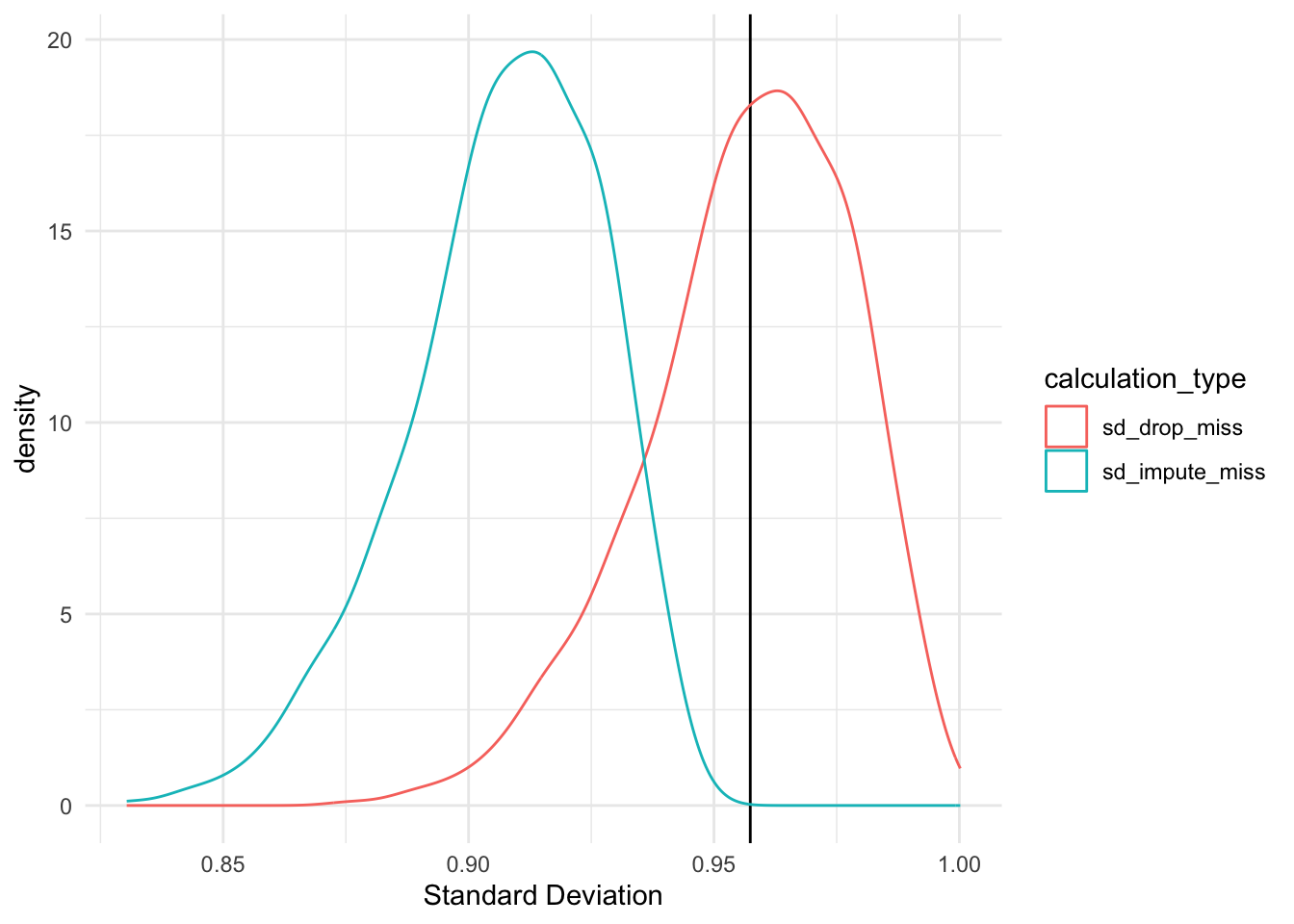
Because the determine above exhibits, there’s a important distinction in the usual deviation estimates when calculated utilizing solely noticed values and calculated with lacking values imputed with the imply. The t-test beneath confirms this.

t.take a look at(sd_diffs$sd_drop_miss, sd_diffs$sd_impute_miss)

    Welch Two Pattern t-test

knowledge:  sd_diffs$sd_drop_miss and sd_diffs$sd_impute_miss
t = 54.288, df = 1992.4, p-value < 2.2e-16
different speculation: true distinction in means isn't equal to 0
95 % confidence interval:
 0.04782442 0.05140925
pattern estimates:
imply of x imply of y 
0.9569447 0.9073278 

Now let’s contemplate how imply imputation can influence the estimation of a correlation between two variables. We are going to simulate two variables with a inhabitants correlation of 0.18.

n <- 100
mean_x <- 0
mean_y <- 0
sd_x <- 1
sd_y <- 1
rho <- 0.18

set.seed(2112)
df <- mvtnorm::rmvnorm(
    n = 100,
    imply = c(mean_x, mean_y),
    sigma = matrix(c(sd_x^2, rho * (sd_x * sd_y),
                     rho * (sd_x * sd_y), sd_y^2), 2, 2)) |>
    as.knowledge.body() |>
    dplyr::rename(x = V1, y = V2)

cor.take a look at(df$x, df$y)

    Pearson's product-moment correlation

knowledge:  df$x and df$y
t = 1.8314, df = 98, p-value = 0.07008
different speculation: true correlation isn't equal to 0
95 % confidence interval:
 -0.01504323  0.36527878
pattern estimates:
      cor 
0.1819124 

We are going to now randomly choose 20% of x values to set to NA.

df_miss <- df
df_miss[sample(n, size = 0.2 * n, replace = FALSE),]$x <- NA
cor.take a look at(df_miss$x, df_miss$y)

    Pearson's product-moment correlation

knowledge:  df_miss$x and df_miss$y
t = 1.8392, df = 78, p-value = 0.06969
different speculation: true correlation isn't equal to 0
95 % confidence interval:
 -0.01658176  0.40543327
pattern estimates:
      cor 
0.2038779 

Be aware that the p-value for each the correlation estimated utilizing the whole dataset and estimated with noticed values solely is larger than 0.05 (i.e. we might fail to reject the null that the correlation is 0).

Now we are going to impute the lacking values with the imply and calcualte the correlation.

df_miss[is.na(df_miss$x),] <- imply(df$x, na.rm = TRUE)
cor.take a look at(df_miss$x, df_miss$y)

    Pearson's product-moment correlation

knowledge:  df_miss$x and df_miss$y
t = 2.0582, df = 98, p-value = 0.04223
different speculation: true correlation isn't equal to 0
95 % confidence interval:
 0.007431517 0.384594022
pattern estimates:
      cor 
0.2035525 

We might now reject the null and conclude that there’s a statistically important correlation between x and y although our authentic dataset from which this was simulated was not.

Associated