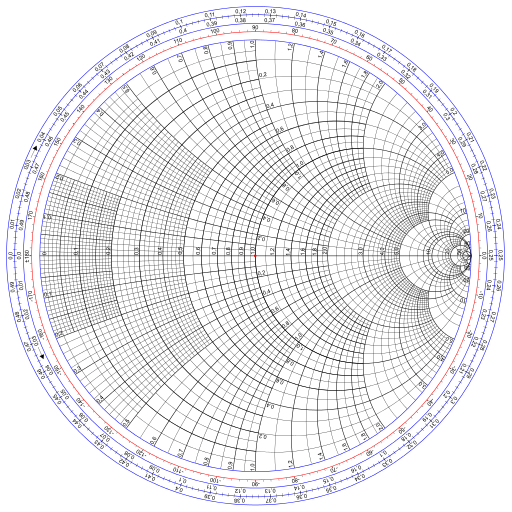
The earlier submit seemed on the fundamentals of the right way to create a Smith chart. The Smith chart is the picture of a Cartesian grid in the precise half-plane below the operate
f(z) = (z − 1)/(z + 1).
On the finish of the submit I famous that evenly distributed grid strains within the z airplane lead to very inconsistently spaced circles on the Smith chart within the w airplane. We will fill within the Smith chart how we please by working backward, ranging from a desired spacing of circles within the chart and tracing them again to the z airplane.
The inverse of the operate f is
g(w) = (1 + w)/(1 − w).
Full circles
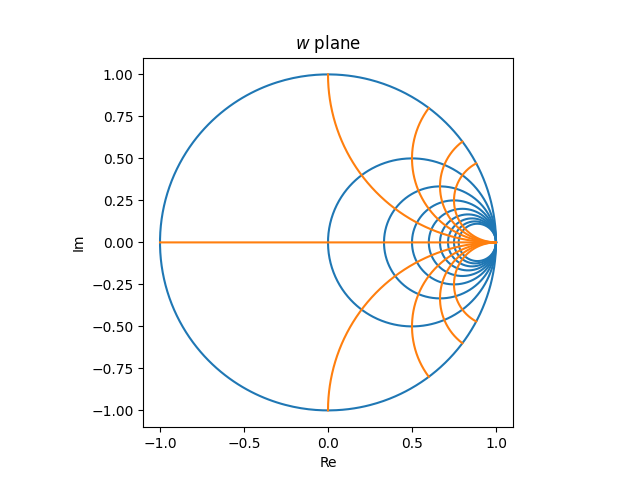
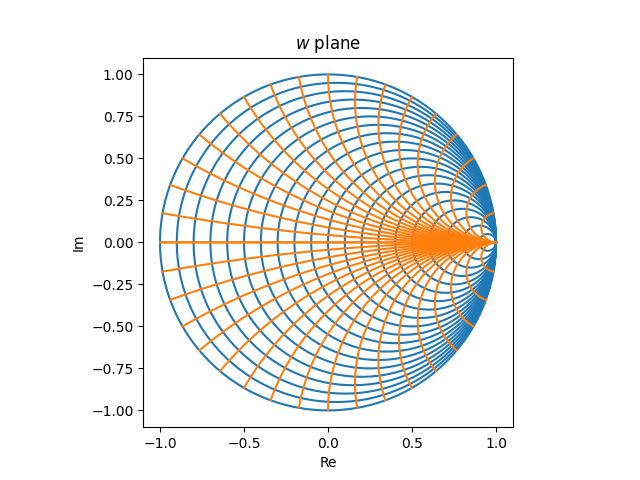
The Smith chart comprises two sorts of circles: circles that match completely contained in the chart, that are the pictures of vertical strains within the z airplane, and circles that stretch outdoors the chart, that are the pictures of horizontal strains. Within the picture under, the previous are blue and the latter are orange.
We will area out the whole (blue) circles how we want and use the inverse transformation g(w) to find out the corresponding spacing of the vertical strains within the z airplane. If we take a degree w0 alongside the horizontal diameter of the Smith chart, w0 is an actual quantity, and so is its inverse z0 = g(w0).
So if we’d just like the intersections of the whole circles with the diameter to be uniformly spaced, we decide uniformly spaced factors wi and use as our vertical strains within the z airplane the strains with actual half g(wi).
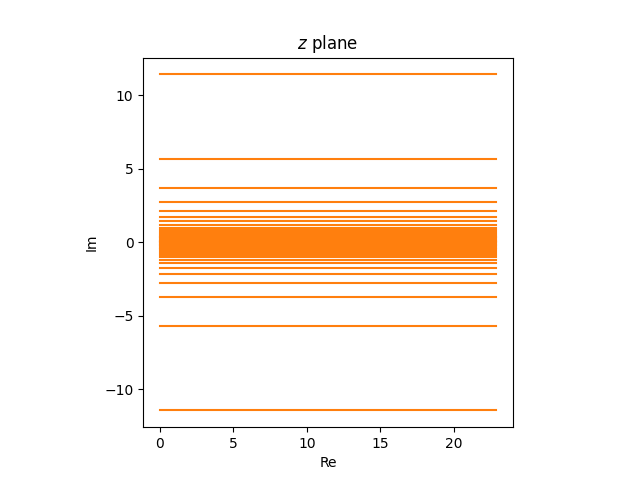
Right here’s the picture we’d get if we wished circles passing by means of the diameter of the Smith chart at increments of 0.1.
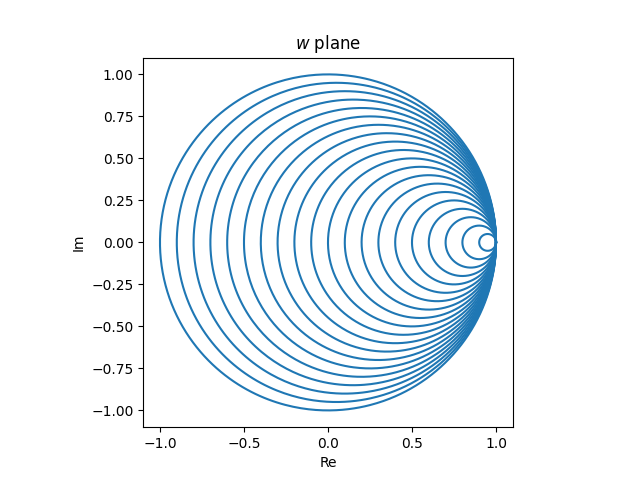
And right here’s the corresponding set of vertical strains within the z airplane that might produce these circles.
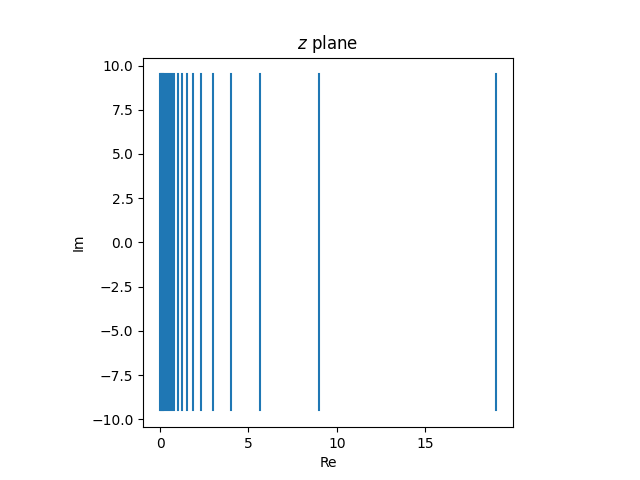
Incomplete circles
Now onto the unfinished circles, the orange circles within the graph above which might be perpendicular to the blue circles.
As we confirmed within the earlier submit, the outer rim of the Smith chart is the picture of the imaginary axis within the z airplane below the operate f(z). So if we decide a degree wi on the rim that we’d like a circle to move by means of, we use the horizontal line with imaginary half equal to g(wi).
So if we wished orange circles to cross the boundary of the Smith chart each 10°, we decide w‘s from the interval [−π, π] spaced π/18 aside.
We will create these strains on the Smith chart under
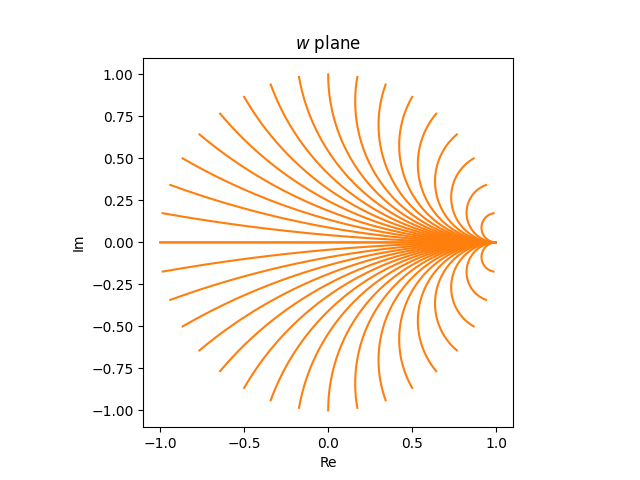
from these strains within the z airplane.
Placing all of it collectively
The picture of this grid within the z airplane
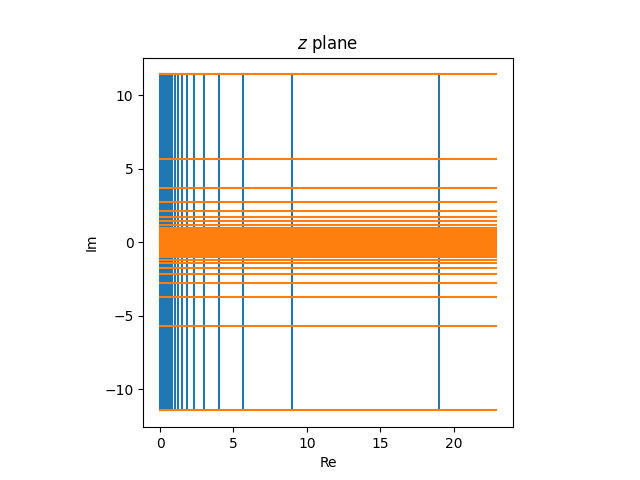
is the next within the w airplane.
Compromise
The Smith charts printed in textbooks use some compromise between even spacing within the w airplane and even spacing within the z airplane.