November 14, 2019
Final evening on the prepare I learn this good paper by David Duvenaud and colleagues. Round midnight I acquired a calendar notification “it is David Duvenaud’s birthday”. So I assumed it is time for a David Duvenaud birthday particular (do not get too excited David, I will not make it an annual custom…)
Background
I not too long ago coated iMAML: the meta-learning algorithm that makes use of implicit gradients to sidestep backpropagating via the inside loop optimization in meta-learning/hyperparameter tuning. The strategy offered in (Lorraine et al, 2019) makes use of the identical high-level thought, however introduces a unique – on the floor much less fiddly – approximation to the essential inverse Hessian. I will not spend quite a lot of time introducing the entire meta-learning setup from scratch, you should use the earlier submit as a place to begin.
Implicit Operate Theorem
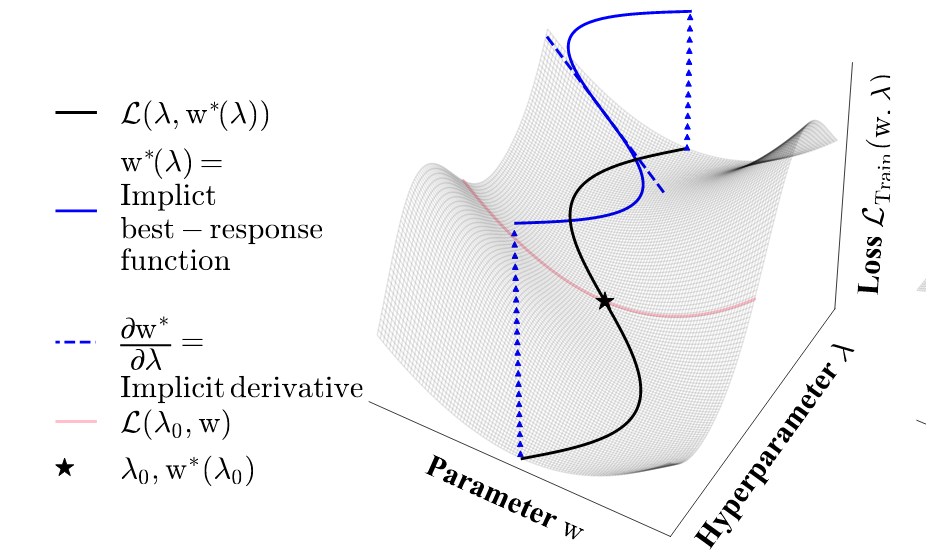
Many – although not all – meta-learning or hyperparameter optimization issues might be said as nested optimization issues. If now we have some hyperparameters $lambda$ and a few parameters $theta$ we’re desirous about
$$
operatorname{argmin}_lambda mathcal{L}_V (operatorname{argmin}_theta mathcal{L}_T(theta, lambda)),
$$
The place $mathcal{L}_T$ is a few coaching loss and $mathcal{L}_V$ a validation loss. The optimum parameter to the coaching downside, $theta^ast$ implicitly is determined by the hyperparameters $lambda$:
$$
theta^ast(lambda) = operatorname{argmin} f(theta, lambda)
$$
If this implicit operate mapping $lambda$ to $theta^ast$ is differentiable, and topic to another situations, the implicit operate theorem states that its by-product is
$$
left.frac{partialtheta^{ast}}{partiallambda}rightvert_{lambda_0} = left.-left[frac{partial^2 mathcal{L}_T}{partial theta partial theta}right]^{-1}frac{partial^2mathcal{L}_T}{partial theta partial lambda}rightvert_{lambda_0, theta^ast(lambda_0)}
$$
The method we obtained for iMAML is a particular case of this the place the $frac{partial^2mathcal{L}_T}{partial theta partial lambda}$ is the id It’s because there, the hyperparameter controls a quadratic regularizer $frac{1}{2}|theta – lambda|^2$, and certainly if you happen to differentiate this with respect to each $lambda$ and $theta$ you’re left with a continuing instances id.
The first problem in fact is approximating the inverse Hessian, or certainly matrix-vector merchandise involving this inverse Hessian. That is the place iMAML and the tactic proposed by Lorraine et al, (2019) differ. iMAML makes use of a conjugate gradient technique to iteratively approximate the gradient. On this work, they use a Neumann sequence approximation, which, for a matrix $U$ appears to be like as follows:
$$
U^{-1} = sum_{i=0}^{infty}(I – U)^i
$$
That is principally a generalization of the higher identified sum of a geometrical sequence: when you’ve got a scalar $vert u vert<1$ then
$$
sum_{i=0}^infty q^i = frac{1}{1-q}.
$$
Utilizing a finite truncation of the Neumann sequence one can approximate the inverse Hessian within the following method:
$$
left[frac{partial^2 mathcal{L}_T}{partial theta partial theta}right]^{-1} approx sum_{i=1}^j left(I – frac{partial^2 mathcal{L}_T}{partial theta partial theta}proper)^i.
$$
This Neumann sequence approximation, a minimum of on the floor, appears considerably much less trouble to implement than operating a conjugate gradient optimization step.
Experiments
One of many enjoyable bits of this paper is the fascinating set of experiments the authors used to show the flexibility of this strategy. For instance, on this framework, one can deal with the coaching dataset as a hyperparameter. Optimizing pixel values in a small coaching dataset, one picture per class, allowed the authors to “distill” a dataset right into a set of prototypical examples. For those who prepare your neural internet on this distilled dataset, you get comparatively good validation efficiency. The outcomes will not be fairly as image-like as one would think about, however for some courses, like bikes, you even get recognisable shapes:
In one other experiment the authors educated a community to carry out information augmentation, treating parameters of this community as a hyperparameter of a studying process. In each of those instances, the variety of hyperparameters optimized have been within the tons of of hundreds, method past the quantity we normally contemplate as hyperparameters.
Limitations
This technique inherits a few of the limitations I already mentioned with iMAML. Please additionally see the feedback the place numerous folks gave tips to work that overcomes a few of these limitations.
Most crucially, strategies primarily based on implicit gradients assume that your studying algorithm (inside loop) finds a singular, optimum parameter that minimises some loss operate. That is merely not a legitimate assumption for SGD the place totally different random seeds would possibly produce very totally different and in a different way behaving optima.
Secondly, this assumption solely permits for hyperparameters that management the loss operate, however not for ones that management different features of the optimization algorithm, akin to studying charges, batch sizes or initialization. For these form of conditions, specific differentiation should be probably the most aggressive resolution. On that observe, I additionally suggest studying this current paper on generalized inner-loop meta-learning and the related pytorch bundle greater.
Conclusion
Pleased birthday David. Good work!