As I’ve written about a number of occasions recently, the Smith chart is the picture of an oblong grid in the proper half-plane beneath the perform
f(z) = (z − 1)/(z + 1).
What would the picture of a grid within the left half-plane seem like?
For starters, since f maps the proper half-plane to the inside of the unit circle, it should map the left-half airplane to the exterior of the unit circle.
As we stated earlier than, the perform f is a Möbius transformation, and so it takes generalized circles, i.e. both a circle or a line, to generalized circles. So the grid traces within the left half-plane are both mapped to traces or circles. Which is it?
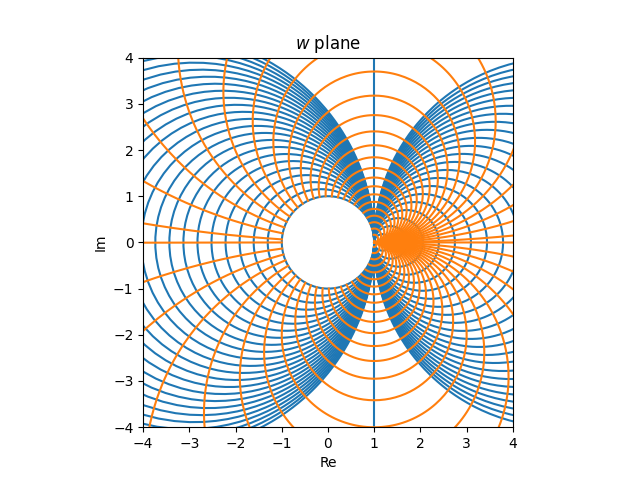
The perform f has a singularity at −1 and so the picture of any line (or circle) via z = −1 is unbounded, i.e. a line, not a circle. Any line not passing via −1 has a bounded picture, which have to be a circle.
The road Re(z) = −1 within the z airplane is mapped to the road Re(w) = 1 within the w airplane. In any other case a vertical line crossing the actual axis at x is mapped to a circle passing via w = (x − 1)/(x + 1). The circle additionally passes via w = 1 as a result of f(∞) = 1. The circle is symmetric about the actual axis, and so that is sufficient info to uniquely decide the circle.
Word that (x − 1)/(x + 1) > 1 when x < −1 and so vertical traces with actual half lower than −1 are mapped to circles to the proper of w = 1. When −1 < x < 0, vertical traces are mapped to circles to the left of w = 1.
The pictures of horizontal traces we’ve checked out earlier than. These are all circles passing via w = 1 and tangent to the circles which are photographs of vertical traces. However this time as a substitute of taking the portion of the circles contained in the unit circle, we take the portion exterior the unit circle.
And with out additional ado, we current the anti-Smith chart, the picture of a grid within the left half airplane.