The “Most Hated” CSS Function: tan()

Final time, we mentioned that, sadly, in response to the State of CSS 2025 survey, trigonometric capabilities are deemed the “Most Hated” CSS characteristic.

That shocked me. I’ll have even been a bit of offended, being a math nerd and all. So, I wrote an article that attempted to showcase a number of makes use of particularly for the cos() and sin() capabilities. Right now, I would like poke at one other one: the tangent perform, tan().

Earlier than attending to examples, we’ve got to ask, what’s tan() within the first place?

The mathematical definition

The only strategy to outline the tangent of an angle is to say that it is the same as the sine divided by its cosine.

Once more, that’s a reasonably easy definition, one which doesn’t give us a lot perception into what a tangent is or how we are able to use it in our CSS work. For now, do not forget that tan() comes from dividing the angles of capabilities we checked out within the first article.

In contrast to cos() and sin() which have been paired with plenty of circles, tan() is most helpful when working with triangular shapes, particularly a right-angled triangle, which means it has one 90° angle:

If we choose one of many angles (on this case, the bottom-right one), we’ve got a complete of three sides:

• The adjoining facet (the one touching the angle)
• The reverse facet (the one away from the angle)
• The hypotenuse (the longest facet)

Talking in these phrases, the tan() of an angle is the quotient — the divided end result — of the triangle’s reverse and adjoining sides:

If the alternative facet grows, the worth of tan() will increase. If the adjoining facet grows, then the worth of tan() decreases. Drag the corners of the triangle within the following demo to stretch the form vertically or horizontally and observe how the worth of tan() modifications accordingly.

Now we are able to begin truly poking at how we are able to use the tan() perform in CSS. I feel a great way to begin is to take a look at an instance that arranges a sequence of triangles into one other form.

Sectioned lists

Think about we’ve got an unordered record of parts we need to prepare in a polygon of some kind, the place every component is a triangular slice of the polygonal pie.

So, the place does tan() come into play? Let’s begin with our setup. Like final time, we’ve got an on a regular basis unordered record of listed record gadgets in HTML:

<ul type="--total: 8">
  <li type="--i: 1">1</li>
  <li type="--i: 2">2</li>
  <li type="--i: 3">3</li>
  <li type="--i: 4">4</li>
  <li type="--i: 5">5</li>
  <li type="--i: 6">6</li>
  <li type="--i: 7">7</li>
  <li type="--i: 8">8</li>
</ul>

Observe: This step will turn out to be a lot simpler and concise when the sibling-index() and sibling-count() capabilities acquire help (and they’re actually neat). I’m hardcoding the indexes with inline CSS variables within the meantime.

So, we’ve got the --total variety of gadgets (8) and an index worth (--i) for every merchandise. We’ll outline a radius for the polygon, which you’ll be able to consider because the peak of every triangle:

:root {
  --radius: 35vmin;
}

Only a smidge of sunshine styling on the unordered record in order that it’s a grid container that locations all the gadgets within the precise heart of it:

ul {
  show: grid;
  place-items: heart;
}

li {
  place: absolute;
}

Now we are able to measurement the gadgets. Particularly, we’ll set the container’s width to 2 instances the --radius variable, whereas every component shall be one --radius huge.

ul {
  /* identical as earlier than */
  show: grid;
  place-items: heart;
  /* width equal to 2 instances the --radius */
  width: calc(var(--radius) * 2);
  /* keep a 1:1 side ratio to kind an ideal sq. */
  aspect-ratio: 1;
}

li {
  /* identical as earlier than */
  place: absolute;
  /* every triangle is sized by the --radius variable */
  width: var(--radius);
}

Nothing a lot to date. Now we have a sq. container with eight rectangular gadgets in it that stack on prime of each other. Meaning all we see is the final merchandise within the sequence for the reason that relaxation are hidden beneath it.

We need to place the weather across the container’s heart level. Now we have to rotate every merchandise evenly by a sure angle, which we’ll get by dividing a full circle, 360deg, by the full variety of parts, --total: 8, then multiply that worth by every merchandise’s inlined index worth, --i, within the HTML.

li {
  /* rotation equal to a full circle divided whole gadgets instances merchandise index */
  --rotation: calc(360deg / var(--total) * var(--i));
  /* rotate every merchandise by that quantity */
  rework: rotate(var(--rotation));
}

Discover, nonetheless, that the weather nonetheless cowl one another. To repair this, we transfer their transform-origin to left heart. This strikes all the weather a bit of to the left when rotating, so we’ll need to translate them again to the middle by half the --radius earlier than making the rotation.

li {
  rework: translateX(calc(var(--radius) / 2)) rotate(var(--rotation));
  transform-origin: left heart;

  /* Not this: */
  /* rework: rotate(var(--rotation)) translateX(calc(var(--radius) / 2)); */
}

This provides us a form of sunburst form, however it’s nonetheless removed from being an precise polygon. The very first thing we are able to do is clip every component right into a triangle utilizing the clip-path property:

li {
  /* ... */
  clip-path: polygon(100% 0, 0 50%, 100% 100%);
}

It form of appears to be like like Wheel of Fortune however with gaps between every panel:

We need to shut these gaps. The following factor we’ll do is enhance the peak of every merchandise in order that their sides contact, making an ideal polygon. However by how a lot? If we have been fidgeting with arduous numbers, lets say that for an octagon the place every component is 200px huge, the proper merchandise peak can be 166px tall:

li {
  width: 200px;
  peak: 166px;
}

However what if our values change? We’d need to manually calculate the brand new peak, and that’s no good for maintainability. As a substitute, we’ll calculate the proper peak for every merchandise with what I hope shall be your new favourite CSS perform, tan().

I feel it’s simpler to see what that appears like if we dial issues again a bit and create a easy sq. with 4 gadgets as an alternative of eight.

Discover that you can imagine every triangle as a pair of two proper triangles pressed proper up towards one another. That’s vital as a result of we all know that tan() is actually, actually good for working with proper angles.

Hmm, if solely we knew what that angle close to the middle is the same as, then we may discover the size of the triangle’s reverse facet (the peak) utilizing the size of the adjoining facet (the width).

We do know the angle! If every of the 4 triangles within the container might be divided into two proper triangles, then we all know that the eight whole angles ought to equal a full circle, or 360°. Divide the total circle by the variety of proper angles, and we get 45° for every angle.

Again to our common polygons, we might translate that to CSS like this:

li {
  /* get the angle of every bisected triangle */
  --theta: calc(360deg / 2 / var(--total));
  /* use the tan() of that worth to calculate good triangle peak */
  peak: calc(2 * var(--radius) * tan(var(--theta)));
}

Now we all the time have the proper peak worth for the triangles, it doesn’t matter what the container’s radius is or what number of gadgets are in it!

And test this out. We are able to play with the transform-origin property values to get totally different sorts of shapes!

This appears to be like cool and all, however we are able to use it in a sensible approach. Let’s flip this right into a round menu the place every merchandise is an possibility you’ll be able to choose. The primary concept that involves thoughts for me is a few form of character picker, kinda just like the character wheel in Grand Theft Auto V:

…however let’s use extra, say, huggable characters:

You could have seen that I went a bit of fancy there and lower the total container right into a round form utilizing clip-path: circle(50% at 50% 50%). Every merchandise continues to be a triangle with arduous edges, however we’ve clipped the container that holds all of them to provide issues a rounded form.

We are able to use the very same concept to make a polygon-shaped picture gallery:

This idea will work possibly 99% of the time. That’s as a result of the maths is all the time the identical. Now we have a proper triangle the place we all know (1) the angle and (2) the size of one of many sides.

tan() within the wild

I’ve seen the tan() perform utilized in plenty of different nice demos. And guess what? All of them depend on the very same concept we checked out right here. Go test them out as a result of they’re fairly superior:

• Nils Binder has this nice diagonal structure.
• Sladjana Stojanovic’s tangram puzzle structure makes use of the idea of tangents.
• Temani Afif makes use of triangles in a bunch of CSS patterns.
• In reality, Temani is a superb supply of trigonometric examples! You’ll see tan() pop up in lots of the issues he makes, like flower shapes or trendy breadcrumbs.

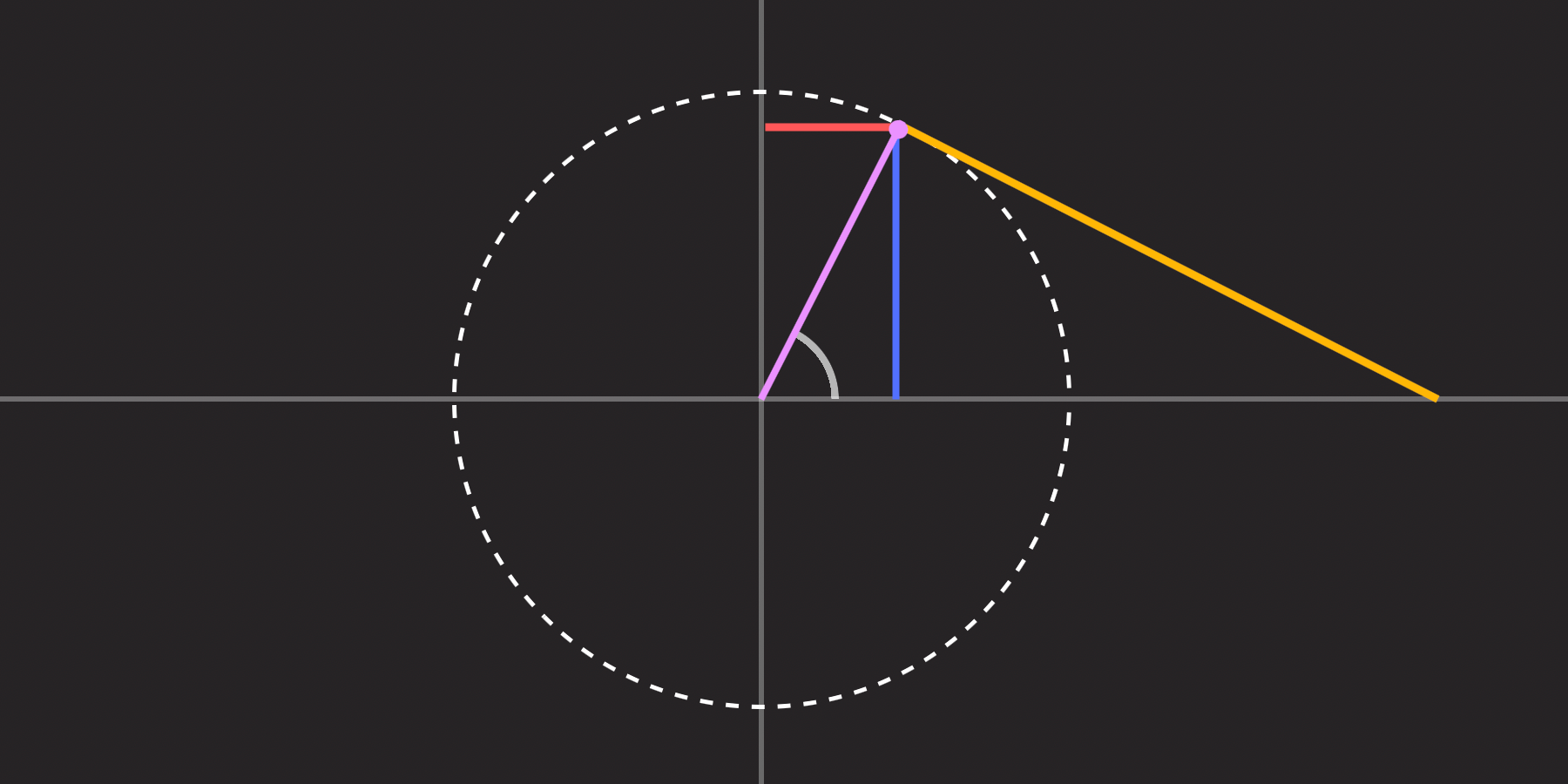
Bonus: Tangent in a unit circle

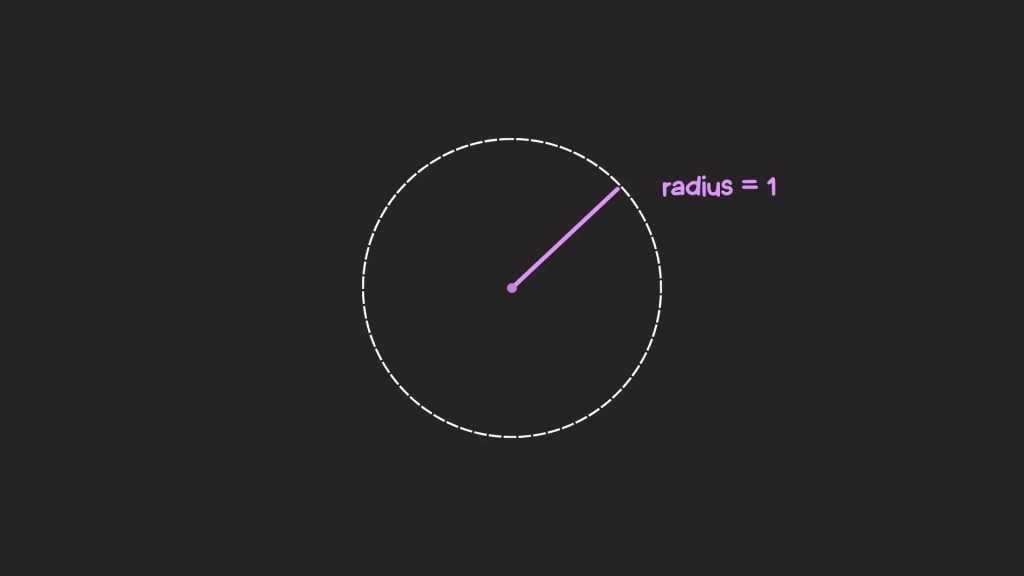
Within the first article, I talked loads concerning the unit circle: a circle with a radius of 1 unit:

We have been capable of transfer the radius line in a counter-clockwise course across the circle by a sure angle which was demonstrated on this interactive instance:

We additionally confirmed how, given the angle, the cos() and sin() capabilities return the X and Y coordinates of the road’s endpoint on the circle, respectively:

We all know now that tangent is said to sine and cosine, due to the equation we used to calculate it within the examples we checked out collectively. So, let’s add one other line to our demo that represents the tan() worth.

If we’ve got an angle, then we are able to forged a line (let’s name it L) from the middle, and its level will land someplace on the unit circle. From there, we are able to draw one other line perpendicular to L that goes from that time, outward, alongside X-axis.

After taking part in round with the angle, chances are you’ll discover two issues:

1. The tan()worth is just constructive within the top-right and bottom-left quadrants. You’ll be able to see why in case you have a look at the values of cos() and sin() there, since they divide with each other.
2. The tan() worth is undefined at 90° and 270°. What will we imply by undefined? It means the angle creates a parallel line alongside the X-axis that’s infinitely lengthy. We are saying it’s undefined because it may very well be infinitely giant to the proper (constructive) or left (unfavourable). It may be each, so we are saying it isn’t outlined. Since we don’t have “undefined” in CSS in a mathematical sense, it ought to return an unreasonably giant quantity, relying on the case.

Extra trigonometry to come back!

To date, we’ve got coated the sin() cos() and tan() capabilities in CSS, and (hopefully) we efficiently confirmed how helpful they are often in CSS. Nonetheless, we’re nonetheless lacking the bizarro world of trigonometric capabilities: asin(), acos(), atan() atan2().

That’s what we’ll have a look at within the third and last a part of this sequence on the “Most Hated” CSS characteristic of all of them.

The “Most Hated” CSS Function: tan() initially revealed on CSS-Methods, which is a part of the DigitalOcean household. It’s best to get the publication.