I noticed one thing yesterday saying that the Japanese bond market had skilled a six normal deviation transfer. This delivered to thoughts a submit I’d written eight years in the past.
All likelihood statements depend upon a mannequin. And in the event you’re likelihood mannequin says an occasion had a likelihood six normal deviations from the imply, it’s extra doubtless that your mannequin is mistaken than that you just’ve really seen one thing that uncommon. I develop on this concept right here.
How doubtless is it {that a} pattern from a random variable will likely be six normal deviations from its imply? When you’ve got in thoughts a traditional (Gaussian) distribution, as most individuals do, then the likelihood is on the order of 1 likelihood in 10,000,000. Six sigma occasions usually are not frequent for any distribution, however they’re not exceptional for distributions with heavy tails.
Let X be a random variable with a Pupil t distribution and ν levels of freedom. When ν is small, i.e. not more than 2, the tails of X are so fats that the usual deviation doesn’t exist. As ν → ∞ the Pupil t distribution approaches the conventional distribution. So in some sense this distribution interpolates between fats tails and skinny tails.
What’s the likelihood that X takes on a worth greater than six normal deviations from its imply at 0, i.e. what does the perform
f(ν) = Prob(X > 6σ)
appear to be as a perform of ν the place σ² = ν/(ν − 2) is the variance of X?
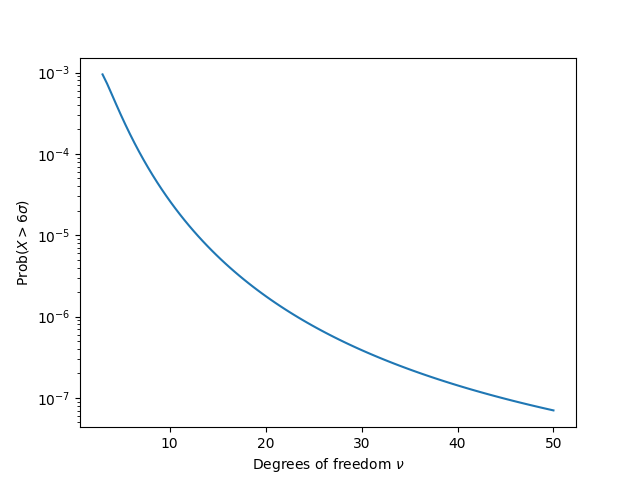
As you’d anticipate, the restrict of f(ν) as ν → ∞ is the likelihood of a six-sigma occasion for a standard distribution, round 10−7 as talked about above. Right here’s a plot of f(ν) for ν > 3. Discover that the vertical axis is on a log scale, i.e. the likelihood decreases exponentially.
What you may not anticipate is that f(ν) isn’t monotone. It rises to a most worth earlier than it decays exponentially. In hindsight this is sensible. As ν → 2+ the variance turns into infinite, and the likelihood of being infinitely removed from the imply is 0. Right here’s a plot of f(ν) between 2 and three.
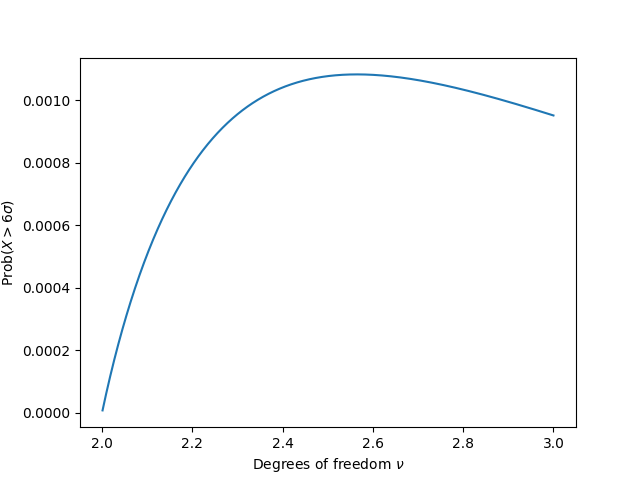
So six sigma chances for a Pupil t distribution rise from 0 as much as a most of round 10−3 then lower exponentially, then asymptotically strategy a worth round 10−7.