Take a deck of playing cards and lower it in half, inserting the highest half of the deck in a single hand and the underside half within the different. Now bend the stack of playing cards in every hand and let playing cards alternately fall from every hand. That is known as a rifle shuffle.
Random shuffles
Persi Diaconis proved that it takes seven shuffles to completely randomize a desk of 52 playing cards. He studied movies of individuals shuffling playing cards with a purpose to assemble a practical mannequin of the shuffling course of.
Shuffling randomizes a deck of playing cards attributable to imperfections within the course of. You could not lower the deck precisely in half, and also you don’t precisely interleave the 2 halves of the deck. Perhaps one card falls out of your left hand, then two out of your proper, and so on.
Diaconis modeled the method with a chance distribution on what number of playing cards are more likely to fall every time. And since his mannequin was lifelike, after seven shuffles a deck actually is nicely randomized.
Good shuffles
Now suppose we take the imperfection out of shuffling. We do lower the deck of playing cards precisely in half every time, and we let precisely one card fall from every half every time. And to be particular, let’s say the primary card will at all times fall from the highest half of the deck. That’s, we do an in-shuffle. (See the following submit for a dialogue of in-shuffles and out-shuffles.) An ideal shuffle doesn’t randomize a deck as a result of it’s a deterministic permutation.
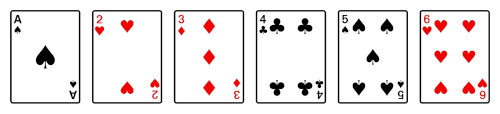
For instance an ideal in-shuffle, suppose you begin with a deck of those six playing cards.
Then you definitely divide the deck into two halves.
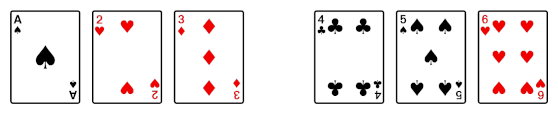
Then after the shuffle you could have the next.

By the way, I created the pictures above utilizing a font that included glyphs for the Unicode characters for enjoying playing cards. Extra on that right here. The font produced black-and-white pictures, so I edited the output in GIMP to show issues purple that ought to be purple.
Coming full circle
In the event you do sufficient excellent shuffles, the deck returns to its unique order. This may very well be the premise for a magic trick, if the magician has the talent to repeatedly carry out an ideal shuffle.
Performing ok excellent in-shuffles will restore the order of a deck of n playing cards if
2ok = 1 (mod n + 1).
So, for instance, after 52 in-shuffles, a deck of 52 playing cards returns to its unique order. We will see this from a fast calculation on the Python REPL:
>>> 2**52 % 53 1
With barely extra work we will present that lower than 52 shuffles received’t do.
>>> for ok in vary(1, 53):
... if 2**ok % 53 == 1: print(ok)
52
The minimal variety of shuffles just isn’t at all times the identical as the dimensions of the deck. For instance, it takes 4 shuffles to revive the order of a desk of 14 playing cards.
>>> 2**4 % 15 1
Shuffle code
Right here’s a operate to carry out an ideal in-shuffle.
def shuffle(deck):
n = len(deck)
return [item for pair in zip(deck[n//2 :], deck[:n//2]) for merchandise in pair]
With this you may affirm the outcomes above. For instance,
n = 14
ok = 4
deck = listing(vary(n))
for _ in vary(ok):
deck = shuffle(deck)
print(deck)
This prints 0, 1, 2, …, 13 as anticipated.